Often we have two or more measured quantities that we combine arithmetically to get some result. Examples include dividing a distance by a time to get a speed, or adding two lengths to get a total length. Now that we have learned how to determine the error in the directly measured quantities we need to learn how these errors propagate to an error in the result.
We assume that the two directly measured quantities are X and
Y, with errors
![]() X and
X and
![]() Y respectively.
Y respectively.
The measurements X and Y must be independent of each other.
The fractional error is the value of the error divided by the
value of the quantity: ![]() X / X
X / X
For many situations, we can find the error in the result Z using three simple rules:
If:
![]()
or:
![]()
then:
![]()
In words, this says that the error in the result of an addition or subtraction is the square root of the sum of the squares of the errors in the quantities being added or subtracted. This mathematical procedure, also used in Pythagoras' theorem about right triangles, is called quadrature.
If:
![]()
or:
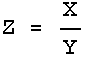
then:
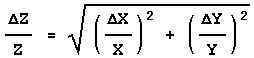
In this case also the errors are combined in quadrature, but this time it is the fractional errors, i.e. the error in the quantity divided by the value of the quantity, that are combined. Sometimes the fractional error is called the relative error.
The above form emphasises the similarity with Rule 1. However, in order
to calculate the value of
![]() Z you would use the following form:
Z you would use the following form:
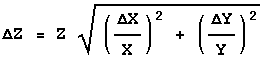
If:
![]()
then:
![]()
or equivalently:
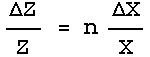
For the square of a quantity, X2, you might reason that this is just X times X and use Rule 2. This is wrong because Rules 1 and 2 are only for when the two quantities being combined, X and Y, are independent of each other. Here there is only one measurement of one quantity.
Question 9.1. Does the first form of Rule 3 look familiar to you? What does it remind you of? (Hint: change the delta's to d's.)
Question 9.2. A student measures three lengths a,
b and c in cm and a time t in seconds:
a = 50 ± 4
b = 20 ± 3
c = 70 ± 3
t = 2.1 ± 0.1
Calculate a + b,
a + b + c, a / t, and (a + c) / t.
Question 9.3. Calculate (1.23 ± 0.03) +
![]() . (
. (![]() is the irrational number 3.14159265…)
is the irrational number 3.14159265…)
Question 9.4. Calculate (1.23 ± 0.03)
×
![]() .
.
Exercise 9.1. In Exercise 6.1 you measured the thickness of a hardcover book. What is the volume of that book? What is the error in that estimated volume?
You may have noticed a useful property of quadrature while doing the above questions. Say one quantity has an error of 2 and the other quantity has an error of 1. Then the error in the combination is the square root of 4 + 1 = 5, which to one significant figure is just 2. Thus if any error is equal to or less than one half of some other error, it may be ignored in all error calculations. This applies for both direct errors such as used in Rule 1 and for fractional or relative errors such as in Rule 2.
Thus in many situations you do not have to do any error calculations at all if you take a look at the data and its errors first.
|
The remainder of this section discusses material that may be somewhat advanced for people without a sufficient background in calculus. |
The three rules above handle most simple cases. Sometimes, though, life is not so simple. The general case is where Z = f(X,Y). For Rule 1 the function f is addition or subtraction, while for Rule 2 it is multiplication or division. Regardless of what f is, the error in Z is given by:

If f is a function of three or more variables, X1, X2, X3, … , then:

The above formula is also used to find the errors for transcendental functions. For example if:
Z = ln(X)
then since the function f is only of one variable we replace the partial derivatives by a full one and:
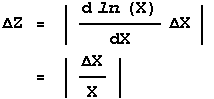
Similarly, if:
Z = sin(X)
then:
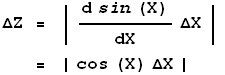
Note that in the above example
![]() X must be in radian measure.
X must be in radian measure.
This document is Copyright © 2001, 2004 David M. Harrison
 |
This work is licensed under a Creative Commons License. |
This is $Revision: 1.18 $, $Date: 2011/09/10 18:34:46 $ (year/month/day) UTC.