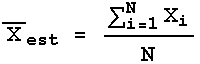
We have seen that when the data have errors of precision we may only estimate the value of the mean. We are now ready to find the error in this estimate of the mean.
Recall that to calculate the estimated mean we use:
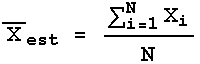
Each individual measurement Xi has the same error,
X, which is usually the estimated standard deviation.
To calculate the error in the numerator of the above equation, we use Rule 1 from Section 9 to write:
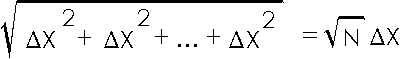
In words, we are combining N quantities
X in quadrature, whose result is the square root of N
times
X.
When we divide the numerator by the denominator N, Rule 2 tells us how to propagate those errors. The denominator has an error of zero, and we have just calculated the error in the numerator. Applying Rule 2, then, gives:
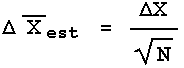
In words, the error in the estimated mean
is equal to the error in
each individual measurement
X divided by the square root of the number of times the
measurement was repeated. Sometimes
is called the standard
error of the mean.
Here is an example. We repeat the measurement of some quantity 4 times and get:
| Result |
|---|
| 1.50 |
| 1.61 |
| 1.39 |
| 1.48 |
The estimated mean of these measurements is numerically 1.4950000 and the estimated standard deviation is numerically 0.0903696 (by numerically we mean the number that is displayed by the calculator). Thus the error in the estimated mean is 0.0903696 divided by the square root of the number of repeated measurements, the square root of 4, which is numerically 0.0451848. So we get:
Value = 1.495 ± 0.045
or:
Value = 1.50 ± 0.04
The fact that the error in the estimated mean goes down as we repeat the measurements is exactly what should happen. If the error did not go down as N increases there is no point in repeating the measurements at all since we are not learning anything about Xest, i.e. we are not reducing its error.
In Section 7 we promised to discuss how many times one should repeat a
measurement. Although one answer is as many times as possible, unless the data
collection is automated and/or you have lots of time and energy, the formula
for
provides another
answer.
If you repeat a measurement 4 times, you reduce the error by a factor of two. Repeating the measurement 9 times reduces the error by a factor of three. To reduce the error by a factor of four you would have to repeat the measurement 16 times. Thus there is a point of "diminishing returns" in repeating measurements. In simple situations, repeating a measurement 5 or 10 times is usually sufficient.
Question 10.1. You are determining the period of oscillation of a pendulum. One procedure would be to measure the time for 20 oscillations, t20, and repeat the measurement 5 times. Another procedure would be to measure the time for 5 oscillations, t5, and repeat the measurement 20 times. Assume, reasonably, that the error in the determination of the time for 20 oscillations is the same as the error in the determination of the time for 5 oscillations. Calculate the error in the period for both procedures to determine which will give the smallest error in the value of the period?
This document is Copyright © 2001 ,2004 David M. Harrison
 |
This work is licensed under a Creative Commons License. |
This is $Revision: 1.8 $, $Date: 2004/07/18 16:41:07 $ (year/month/day) UTC.