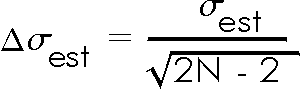
Imagine we have some sample of 10 datapoints which we assume are normally distributed. The estimated standard deviation is numerically equal to 0.987654321, which is larger than the reading error for these measurements. (By "numerically" we mean that is what the calculator read when we computed the standard deviation.) Since the estimated standard deviation is larger than the reading error, it will be the error in the value of each of the datapoints.
As mentioned at the end of Section 5, when a sample has N datapoints the expected uncertainty in the estimated standard deviation is:
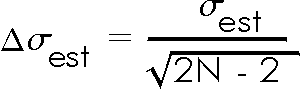
For this data, the error is numerically equal to 0.232792356, which is 23% of the value of the estimated standard deviation. This relatively high percentage is another way of expressing what you saw in Exercise 5.1, where even 50 repeated trials of the number of radioactive decays in one second was not a "large number" for data which have a significant spread.
What these numbers are saying is that we think the actual value of the standard deviation is probably greater than 0.987654321 - 0.232792356 = 0.704861965, and is probably less than 0.987654321 + 0.232792356 = 1.220446677. A moment's thought about this should convince you that many of the digits in the estimated standard deviation have no significance.
In fact, the value of the estimated standard deviation is something like: 0.99 ± 0.23 or maybe even 1.0 ± 0.2. Certainly 0.988 ± 0.233 has more digits in both the value and its error than are actually significant.
Examining the above formula for the error in the estimated standard deviation indicates that even if one repeats a measurement 50 times, the error in the estimated standard deviation is about 10% of its value. Put another way, even for N equal to 50 the estimated standard deviation has at most only two digits that have any meaning.
Imagine one of the data points has a numerical value of 12.3456789. Then if we take the estimated standard deviation to be 0.99, then the data point has a value of 12.35 ± 0.99, i.e. probably between 11.36 and 13.34. It would be wrong to say 12.345 ± 0.99, since the '5' has no meaning. It would also be wrong to say 12.35 ± 0.987, since the '7' similarly has no meaning. These examples illustrate a general conclusion:
For experimental data the error in a quantity defines how many figures are significant.
In the case where the reading error is larger than the estimated standard deviation, the reading error will be the error in each individual measurement. However as we saw in the previous section, the reading error is little more than a guess made by the experimenter. I do not believe that people can guess to more than one significant figure. Thus a reading error almost by definition has one and only one significant figure, and that number determines the significant figures in the value itself.
Above we saw that even if one repeats a measurement 50 times the standard deviation has at most two significant figures. And now we have seen that the reading error certainly does not have more than two significant figures. So in general:
In simple cases errors are specified to one or at most two digits.
Question 8.1. Express the following quantities to the correct number of significant figures:
(a) 29.625 ± 2.345
(b) 74 ± 7.136
(c) 84.26351 ± 3
This document is Copyright © 2001, 2004 David M. Harrison
 |
This work is licensed under a Creative Commons License. |
This is $Revision: 1.10 $, $Date: 2011/09/10 18:34:46 $ (year/month/day) UTC.