In the previous section we
saw that when we repeat measurements of some quantity in which random
statistical factors lead to a spread in the values from one trial to the next,
it is reasonable to set the error in each individual measurement equal to the
standard deviation of the sample.
Here we discuss another error that arises when we do a direct measurement of some quantity: the reading error.
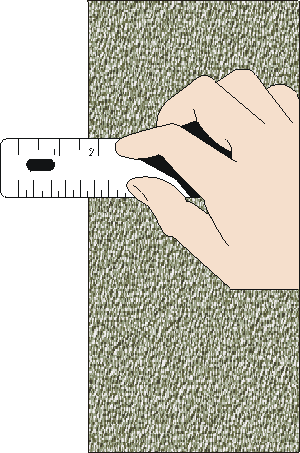
For example, to the right we show a measurement of the position of the left hand side of some object with a ruler. The result appears to be just a bit less than 1.75 inches.
We shall assume that the ruler is perfectly constructed. This assumption is discussed further in Section 12.
To determine the reading error in this measurement we have to answer the question: what is the minimum and maximum values that the position could have for which we will not see any difference? There is no fixed rule that will allow us to answer this question. Instead we must use our intuition and common sense.
Could the value actually be as large as 1.75? Perhaps, but almost certainly no larger. Could the value be as small as 1.70? Very unlikely. How about 1.73? Perhaps, but probably no smaller. Thus a reasonable estimate of the reading error of this measurement might be ± 0.01 inches. Then we would state that the position is 1.74 ± 0.01 inches.
For your eyes and computer monitor with which you are looking at the above measurement, you may wish to instead associate a reading error of 0.02 inches with the position; this is also a reasonable number. A reading error of 0.03 inches, though, is probably too pessimistic. And a reading error much less than 0.01 is probably too optimistic.
|
To the right we show the same measurement, but with two differences. First it is smaller. Second the person doing the measurement needs to clean their glasses. It seems fairly obvious that the reading error for this measurement will be larger than for the previous one. |
 |
We assume that the reading error indicates a spread in repeated measurements, just like the standard deviation discussed in the previous section. However, here natural human biases means that each repeated measurement should be done by a different person. So if we get a collection of objective observers together to look at the first measurement above, we expect most but perhaps not all observers will report a value between 1.73 and 1.75 inches. (Of course, in real life seldom if ever do we actually get a collection of observers together so that we may determine the reading error of a simple measurement.)
Note that there is often a trade-off when assigning a reading error such as above. On the one hand we want the error to be as small as possible, indicating a precise measurement. However we also want to insure that measured value probably lies within errors of the "true" value of the quantity, which means we don't want the error to be too small.
Exercise 6.1. Choose your textbook or some other hardcover book and measure its thickness. What is the reading error in this measurement? Repeat the measurement a few times at different places on the book. What is the estimated standard deviation of your measurements?
For a measurement with an instrument with a digital readout, the reading error is "± one-half of the last digit."
|
We illustrate with a digital thermometer shown to the right. The phrase "± one-half of the last digit" above is the language commonly used in manufacturer's specification sheets of their instruments. It can be slightly misleading. It does not mean one half of the value of the last digit, which for this example is 0.4. It means one-half of the power of ten represented in the last digit. Here, the last digit represents values of a tenth of a degree, so the reading error is 1/2 x 0.1 = 0.05. This is saying that the value is closer to 12.8 than to 12.7 or 12.9. It assumes that the engineer who designed the instrument has made it round measurements correctly in the display. Finally, then we would write the temperature as 12.80 ± 0.05 oC. |
 |
 |
One sometimes sees statements that the reading error of an analog instrument such as a meter stick is something like ± one-half of the smallest scale marking. These and similar statements are wrong! The reading error of such an analog instrument can only be determined by the person reading the instrument, and can sometimes be different for different people. | |
This document is Copyright © 2001, 2004 David M. Harrison
 |
This work is licensed under a Creative Commons License. |
This is $Revision: 1.8 $, $Date: 2004/07/18 16:46:52 $ (year/month/day) UTC.