PHY138Y - Mechanics - Class 13 - Wednesday October 25, 2006

Introduction

"Music is a hidden practice of the soul, which does not know that it is doing mathematics."

-- Leibniz

Test Review

The class on Monday, October 31, will be a review for the test. It will be all PowerPoint based. You may access a pdf of the PowerPoint with the button to the right.

Today's Class

Supplementary Notes

We discussed forces on the hip. Supplementary Notes in pdf format are available on this topic.

In-Class Question

We asked only one "clicker" question today.

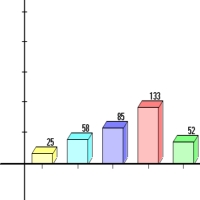
The distribution of your answers is shown to the right. Only about one-quarter of you got this correct: C. The mass of the meter stick is one kg. As usual, it is better we found out about this mis-understanding now instead of on the test. In class I discussed two ways of arriving at the correct answer.

You may wish to check your understanding with the following.

Simple Suggested Problem

In class we discussed the answer by talking about the torques acting about the actual pivot point. However, since the meter stick and rock are in equilibrium the torques can be evaluated about any point. To analyse about any other point you will need to think about the force exerted on the meter stick by the pivot. The total vertical force acting on the meter stick plus rock is equal to zero.

1. Evaluate the torque about the left side of the meter stick to conclude that the mass of the meter stick is 1 kg.
2. Evaluate the torque about the right side of the meter stick to conclude that the mass of the meter stick is 1 kg.

Flash Animations

We used two Flash animations today.

This one illustrates the "right hand screw rule" When the fingers of the right hand curl in the direction of rotation of the screw, the thumb points in the direction that the screw moves. It is also pointing in the direction of the angular velocity vector of the rotating screw.
This is a very simple little animation showing the direction of the angular velocity vector for a rotating wheel.

It is perhaps worth emphasising something I tried to stress in class today. Symmetry considerations lead us to assign the direction of the angular velocity vector to lie along the axis of rotation. Then which of the two possible directions it can point is just a convention.

Other Class Materials

Pdf version of the PowerPoint on the side screens.
Today's Journal.

The arrows let you jump to the previous/next class summaries.