The Theories of Relativity
These Course Notes are a supplement to the treatment of Relativity in Chapter
37 of the PHY132H textbook, Randall D. Knight, Physics for Scientists
and Engineers, 2nd ed. (Pearson Addison-Wesley, 2008). The text remains
our primary reference for this discussion. Here we will explore some of the
conceptual foundations of Relativity. We will also briefly introduce the General
Theory of Relativity, which is not discussed in the textbook.
There are two different theories of Relativity which are due to Einstein:
- The Special Theory of 1905. This theory considers observers who are in
uniform relative motion.
- The General Theory of 1916. This theory considers observers who are in
any state of relative motion, including relative acceleration. This will
turn out to also be a theory of gravitation.
Below, discussion of Special Relativity will reference the section numbers
of the text where this supplementary material is relevant. For the discussion
of General Relativity, with the exception of the Principle of Equivalence sub-section
of §13.3
the text does not discuss this topic so no section numbers can be given.
A: §37.3 - Einstein's Principle of Relativity
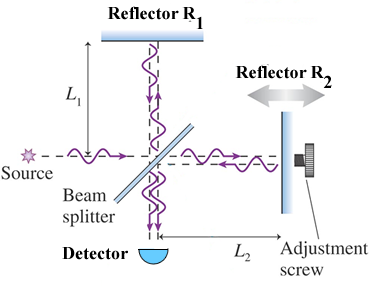
You will recall the discussion of the Michelson Interferometer in
Chapter 22. The figure is slightly modified from Fig. 22.20 of the text.
A wave from the Source is split into two equal intensity parts
by the Beam Splitter, sent to the two Reflectors, and returned to the Beam
Splitter. Half of those returned rays are sent to the Detector.
Such an interferometer can be used with light waves, sound waves, or
any other kind of wave. For a sound wave, the Source is a loudspeaker, the
Beam Splitter can be just a piece of paper, the Reflectors can be glass
plates, and the Detector is a microphone. |
 |
If the distances from the Beam Splitter to the Reflectors, L1 and L2,
are equal then the two waves will constructively interfere at the Detector provided
the interferometer is stationary relative to the medium through which the waves
are traveling.
Imagine we have constructed an interferometer for sound waves. Then if the
arms of the interferometer have equal lengths and there is no wind blowing,
we get constructive interference: the time it takes the two sound waves
to travel from the Beam Splitter to the Reflectors and back to the Beam Splitter
are equal. But if a constant wind of speed v is blowing from left
to right then the time it takes the two waves to travel to the Reflectors and
back will be unequal. If we call the speed of sound relative to the air c (343
m/s, not the speed of light!) then it is fairly simple to show that:
Imagine that with the wind blowing we have adjusted the lengths L1 and L2 to
compensate for the different times it takes for the sound waves to travel to
and from the two Reflectors so we get a maximum sound intensity at the Detector.
Then if we slowly rotate the whole interferometer the carefully adjusted lengths
will no longer give us constructive interference and, depending on the speed
of the wind v, we
could see the sound intensity go from maximum to minimum to maximum etc.
As discussed in the text, in the 19th century physicists thought about a medium
for light which was called the ether. Presumably the ether is stationary
relative to the fixed stars. But the surface of the Earth is not stationary
relative to the fixed stars: it is rotating on its axis, in orbit around the
Sun, and the whole solar system is moving towards the constellation Hercules.
So on the surface of the Earth there will be an "ether wind" with
a speed, depending on the time of day and season, as large as 3.0 x 104 m/s.
In the 1880's Michelson and Morley constructed a light interferometer
to attempt to measure the speed of the ether wind relative to the surface
of the Earth. The lengths of the arms of the interferometer were 10
m. To minimise vibration the whole apparatus was mounted on a marble
block floating in a tub of mercury. They adjusted the interferometer
for constructive interference, and then gently rotated the interferometer
by 90 degrees. They calculated that they should easily see the combined
beams going through fringe shifts in the interference pattern as
they rotated the apparatus.
|
 |
When they did the experiment, they got no result: the interference pattern
did not change! It was suggested that maybe the speed of the earth due to its
rotation on its axis was canceling its speed due to its orbit around the sun.
So they waited 12 hours and repeated the experiment. Again they got no result.
It was suggested that the Earth's motion in orbit around the Sun cancelled
the other motions. So they waited six months and tried the experiment again.
And again they got no result. It was suggested that maybe the mass of the earth "dragged" the
ether along with it. So they hauled the apparatus up on top of a mountain,
hoping that the mountain would be sticking up into the ether that was not being
dragged by the earth. And again they got no result. Thus, this attempt to measure
the motion of the earth relative to the ether failed.
Lorentz was among many who were very puzzled by this result. He proposed that
when an object was moving relative to the ether, its length along its direction
of motion would be contracted by just the right amount needed to explain the
experimental result. If the length of the object when it is at rest with respect
to the ether is L0, then if it is moving at speed
v through
the ether its length L along its direction of motion relative to
the ether is:
Here c is the speed of light, not the speed of sound. So
when the interferometer is oriented as in the figure and an ether wind is
blowing from left to right, L2 is
contracted but L1 is
not.
When Einstein was 16, in 1895, he asked himself an interesting question:
"If I pursue a beam of light with the velocity c I should observe such a beam
of light as a spatially oscillatory electromagnetic field at rest. However,
there seems to be no such thing, whether on the basis of experience or according
to [the theory of electricity and magnetism]. From the very beginning it appeared
to me intuitively clear that, judged from the standpoint of such an observer,
everything would have to happen according to the same laws as for an observer
who, relative to the earth, was at rest. For how, otherwise, should the first
observer know, i.e.. be able to determine, that he is in a state of uniform
motion?" -- As later written by Einstein in "Autobiographical Notes", in
Schilpp, ed., Albert Einstein: Philosopher-Scientist .
He continued to work on this question for 10 years with the mixture of concentration
and determination that characterised much of his work. He published his answer
in 1905:
"... light is always propagated in empty space with a definite velocity c
which is independent of the state of [relative] motion of the emitting body
.... The introduction of a `luminiferous ether' will be superfluous inasmuch
as the view here to be developed will not require an `absolutely stationary
space' provided with special properties." -- Annalen Physik 17 (1905).
Put another way, the speed of light is 3 x 108 m/s with respect
to all observers.
Notice that this explains the null result of the Michelson-Morley
experiment. However, although the evidence is not certain it seems quite likely
that in 1905 Einstein was unaware of the experiment (cf. Gerald Holton, "Einstein,
Michelson and the 'Crucial' Experiment," which has appeared in Thematic
Origins of Scientific Thought , pg. 261. and also in Isis 60 ,
1969, pg. 133).
| A Flash animation of the Michelson-Morley Experiment by Wan-Ching Hui
at the University of Virginia is available via the blue button to the right.
It will open in a separate tab/window. |
 |
B: §37.6 - Time Dilation
When we discussed the Doppler effect ( §20.7) we deferred discussion
of the Doppler Effect for Light Waves sub-section. We are
now ready to discuss this topic.
For mechanical waves, we made a distinction between two different cases:
- The observer is stationary relative to the medium and the source is moving
relative to the medium. This is described by Equation 20.39.
- The source is stationary relative to the medium and the observer is moving
relative to the medium. This is described by Equation 20.40.
For light waves there is no medium, so the distinction between these cases
disappears: only the relative motion of the source and observer count.
For the reference frame of the observer the textbook's Figure 20.26 applies.
We will discuss what Pablo measures.
Just as for the non-relativistic case, the wavelength is greater for Pablo
than for an observer stationary relative to the source: the wave is "stretched".
However there is another factor for the relativistic case: the period T of
the source is greater than the period T0 of the source
relative to an observer stationary relative to the source by the factor  defined
by Equation 37.22. This second effect, due to relativistic time dilation, is
what we were not able to discuss when we first talked about the Doppler effect.
defined
by Equation 37.22. This second effect, due to relativistic time dilation, is
what we were not able to discuss when we first talked about the Doppler effect.
A homework problem will let you show that the relativistic Doppler effect,
Equation 20.41, is correct.
C: §37.7 - Length Contraction
C.1 The Spacetime Interval Sub-Section
This sub-section of the text begins by discussing two students with rotated
reference frames. Here I will extend the analogy: The Parable of the Surveyors.
Once upon a time there was a kingdom in which all positions were measured
relative to the town square of the capitol.
This kingdom had a sort of
strange religion that dictated that all North-South distances were to
be measured in sacred units of feet; East-West distances were
measured in everyday units of meters . Despite this religious
requirement all positions in the kingdom could be uniquely specified.
There were two schools of surveying in operation. One, the daytime school,
used a compass to determine the direction of North. The other, the nighttime school,
used the North star to determine the direction of North. As the sophistication
of the measuring instruments increased, people began to notice that the
daytime and nighttime measurements didn't quite agree. This is because
magnetic North as determined by a compass is not in exactly the same
direction as the North star. The figure to the right illustrates, although
the actual difference is much less than in the diagram. |
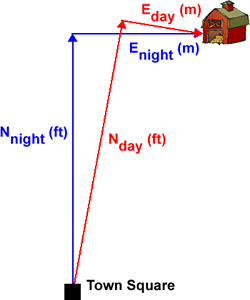 |
Finally, a young fellow named Albert attended both schools of surveying. He
was also an irreligious person so did not take the religious requirement
of measuring North-South distances in sacred units of feet seriously. To the
consternation of the priests, he converted those North-South distances to everyday
units by multiplying by k,
the number of meters in a foot. He then discovered that although the daytime
and nighttime numbers for the position of a particular place differed slightly,
there was a combination of the measurements that was constant:
What he is calculating, of course, is the distance squared between the town
square and a particular location using Pythagoras' Theorem. You may wish to
notice that there is no subscript on k: the conversion from feet
to meters is the same for both schools of surveying.
The text shows that for two observers, say Sue and Lou, in relative motion
who measure the time between two events and the distance between the same two
events there is also a constant quantity. Here is Eqn. 37.19 of the text written
in a more suggestive form:
Notice that except for the minus sign, the form of this expression is very
similar to the expression relating the daytime and nighttime measurements.
One of the conclusions, then is:
The speed of light is only a conversion factor for units.
If we had started out measuring time in everyday units of meters instead of
sacred units of seconds, the speed of light would be exactly one. A time of
1 meter is the time it takes light to travel a distance of 1 meter.
Stop To Think C.1
Astronomers often measure lengths in units of light years. Say we
measure time in units where the value is exactly one for the time it takes
light to travel one light year. What is this unit for time?
C.2 Spacetime Diagrams
Here we discuss a useful way of visualising the nature of spacetime in Special
Relativity: the spacetime diagram.
The time axis is vertical, and of course we have multiplied t by c so we are
measuring time in meters, the same as the other coordinates.
The plot of time versus position for some object is called the worldline.
Since we are not using "religious" units to measure time, the
speed of light is exactly one. Therefore the worldline of an object moving
at c makes an angle of 45 degrees, and is called the light
cone.
A worldline for an object moving at less than the speed of light and that
is at x =
0 at t =
0 is shown in purple.
The point x = 0 and t = 0 is called the present.
The region of spacetime inside the light cone for positive values of the
time is called the future. The region of spacetime inside the light
cone for negative values of the time is called the past.
|
 |
We
can not know what happened at the star Alpha Centauri yesterday; it is about
4 light years away and since no information can travel faster than the speed
of light we will have to wait four years to find out what happened there. Thus
the coordinate of Alpha Centauri yesterday, which is outside the light cone,
is inaccessible to us located in the present. Similarly, we can not send a
signal to Alpha Centauri that will arrive tomorrow. Thus the entire region
of spacetime outside the light cone is called elsewhere
Stop To Think C.2
What is the orientation of a worldline for an object that is stationary? You
may wish to specify your answer in terms of the angle it makes with the x axis.
C.3 The Significance of the Minus Sign
In our discussion of the text's Spacetime Interval sub-section
we saw that the equation relating coordinates in rotated reference frames,
Eqn. C.1, has a very similar structure as the Relativistic one relating
the time and distance between two events for two observers in relative
motion, Eqn C.2., except that in Eqn C.2 there is an overall minus sign
between the time and distance parts. The significance of the minus sign
is that the space and time axes of the spacetime diagrams for the two
observers, Sue and Lou, are rotated towards each other.
The angle between the axes is related to the relative speeds v of
the observers by:
|
 |
C.4 The Dimensions of Spacetime
| There is a problem with the spacetime diagram: it only has one explicit
spatial coordinate x . The way the light cone is drawn
suggests, properly, that there is a second spatial coordinate, say y ,
that points out of the plane of the figure. Drawing a spacetime diagram
with two spatial coordinates plus a time coordinate is not that difficult
and an example is given to the right. But how do we indicate the third
spatial coordinate, say z? |
 |
The following figures indicate one way to approach a representation of such
a four-dimensional object.
We begin with a zero-dimensional object, a point. |
 |
We move the point one unit to the right to generate a one-dimensional
line. |
 |
Moving the line one unit perpendicular to itself generates a two-dimensional
square. |
 |
We move the square one unit perpendicular to itself, and we represent
the three dimensional cube as shown. |
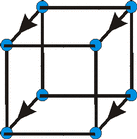 |
Finally, if the moving of the square down and to the left was used
to get from a square to a cube, then we represent moving the cube perpendicular
to itself as moving it down and to the right. The result is called a tesseract . |
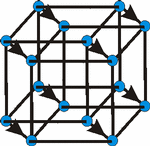 |
In about 1884 Edwin Abbott wrote a lovely little book called Flatland:
a Romance of Many Dimensions ; the book has been reprinted many
times and is readily available. In it he imagines a world with only two spatial
dimensions. One of Flatland's inhabitants, named A. Square , became
aware of the existence of a third spatial dimension through an interaction
with a higher dimensional being, a Sphere. He attempted to explain
this third dimension to the other inhabitants of Flatland, which of course
promptly got him put in jail. The difficulties A. Square had in visualising
the third spatial dimension is analogous to the difficulties we have in visualising
a four-dimensional spacetime.
| A very simple Flash animation of the interaction of the Sphere with Flatland
is available via the blue button to the right. It will appear in a separate
tab/window. |
 |
| There is also a lovely video which explores the idea of Flatland, which
may be accessed via the link to the right. Running time: 5:11. |
 |
| Here is another video about Flatland, which extends the discussion to
tesseracts. It is by Carl Sagan. Running time: 7:15. |
 |
C.5 More Spacetime Diagrams and Some Discussion
The spacetime diagram to the right was drawn by Claude Bragdon in
1913 for his book A Primer of Higher Space. In this figure
the time axis is horizontal.
Bragdon's "day job" was as an architect. He, along with Abbott, also
believed that learning to comprehend a fourth dimension was in some sense
equivalent to enlightenment. Bragdon designed many buildings in Rochester
New York on which the tesseract can be found.
|
 |
Here is another spacetime diagram, this time from D. Postle, Fabric
of the Universe , pg. 106. It can be seen that different observers
slice spacetime, the frames of the movie, in different ways.
We imagine our worldline in this spacetime diagram. Then, as David Park
wrote, "our consciousness crawls along our worldline as a spark burns along
a fuse" (in J.T. Fraser et al., eds., The Study of Time,
pg. 113). As it crawls up our worldline we discover new slices of spacetime. |
 |
Louis de Broglie wrote a famous commentary on the worldview of the theory
of relativity:
"In space-time, everything which for each of us constitutes the past, the
present, and the future is given in block, and the entire collection of events,
successive for us, which form the existence of a material particle is represented
by a line, the world-line of the particle .... Each observer, as his time passes,
discovers, so to speak, new slices of space-time which appear to him as successive
aspects of the material world, though in reality this ensemble of events constituting
space-time exist prior to his knowledge of them." -- in Albert Einstein:
Philosopher-Scientist , pg. 114.
Dogen Zenji seemed to have a similar view 800 years ago.
"It is believed by
most that time passes; in actual fact it stays where it is. This idea of
passing may be called time, but it is an incorrect idea, for since one only
sees it as passing, one cannot understand that it stays just where it is.
In a word, every being in the entire world is a separate time in one continuum." -- Shobogenzo.
Einstein wrote when his friend Besso died, "For us believing physicists, the
distinction between past, present, and future is illusion, however persistent."
We conclude this part of our discussion on the meaning of spacetime
with a famous Zen story.
Two Zen monks were arguing about a flag waving in the breeze, and whether it
was the flag or the wind that was moving. The Sixth Patriarch of Zen, Hui Neng,
overheard; "I suggested it was neither, that what moved was their own mind."
A commentary by Mumon may be appropriate:
Wind, flag, mind moves.
The same understanding.
When the mouth opens
All are wrong.
C.6 Addition of Velocities
In §37.8 the textbook shows that velocities for different observers do
not transform as expected by our common sense. This section of
the textbook and its main topic, the Lorentz transformation, are not part of
the syllabus for this course. In this little section I derive the same result
as the text, but use only the fact that the speed of light is the same value
for all observers.
| We imagine Lou watches a train go by with speed v. For him the
length of the train is L. On the left side of the train a pulse of light
travels towards the front of the train at speed c, and an everyday particle
travels towards the front of the train at speed uLou < c.
There is a mirror on the front of the train. |
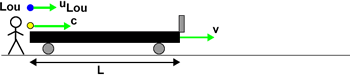 |
| At a time t1 the light is reflected from the mirror. |
 |
| At a time t2 later the light pulse meets the particle.
They meet behind the front of the train by some fraction f of the full
length of the train |
 |
The fraction f is some number between 0 and 1, and will have the same value
for all observers. Perhaps there is an array of sensors on the floor of the
train and one of the them lights up when the light and the particle
meet up. All observers will agree on which sensor is lit, and therefore the
value of f.
The total distance the particle moved from the start of the race to its encounter
with the light is equal to the distance the light moved in going from the rear
to the front minus the distance it moved in going from the front back to the
particle.
The distance the light traveled in going from the rear to the front is just
the length of the car plus the distance the train moved.
The distance the light traveled in going from the front to where it met the
particle is the distance from the front of the train to the meeting point minus
the distance the train moved.
Eliminating L from Eqns C.5 and C.6 and combining with Eqn C.4 gives
Nowhere have we assumed that the speed of the train is non-zero. Therefore
Eqn. C.7 is also valid for an observer, Sue, who is riding on the train.
Equating Eqns. C.7 and C.8 gives
This is the same as the first version of the textbook's Equation 37.30 except
for different notation.
A Geometrical Approach to Addition of Velocities
There is a geometrical way to add velocities in Special Relativity. We will
use the situation illustrated by the textbook's Figure 37.33a and the equation
is the second of the textbook's Equation 37.30.
To add the velocities geometrically uses four steps:

Step 1: Construct a circle with radius 1. The horizontal axis will be
the speeds divided by the speed of light. |

Step 2. On the horizontal axis, indicate the speeds u' and v
with dots .
In this example these are +0.4 c and +0.6 c. |

Step 3. Draw a line from (0,1) through one of the dots to the circle,
and draw another line from (0, -1) through the other dot to the circle.
Which line goes through which dot does not matter. |

Step 4. Draw a line that connects where the two lines from Step 3 meet
the circle. Where this line intersects the hozizontal axis is the speed
u divided by c. |
D: General Relativity
This topic is not discussed in the textbook.
D.1 Three "Easy" Pieces
Einstein used three different ideas to build the General Theory of Relativity,
which we describe here.
Piece 1 - Geometry is Physics
To the right are shown a distant star, the Sun, and Earth. Clearly the
figure is not drawn to scale.
There is a straight dotted line connecting the star and the Earth. Imagine
a light ray that leaves the star along the dotted line: it is headed
directly for the Earth. Will that light ray actually reach the Earth?
|
 |
Let us think for a moment about the equation E = mc2.
We know that light has energy, and therefore it has mass. And all masses
are attracted gravitationally by all other masses. So the light energy that
left the star along the dotted line will be attracted gravitationally by the
mass of the sun, which will cause its path to be deflected as shown. Thus that
light ray from the star does not reach the Earth. It is the upper trajectory
in the figure that represents the light from the Star that reaches the Earth.
But the definition of a straight line is that it is the shortest
distance between two points. And we also know that light rays are the fastest
way of getting information from, say, the star to the Earth. Thus, the upper
path in the figure defines a straight line.
We imagine a flat plane as representing all three spatial dimensions plus
the time dimension, a Flatland analogy.
Then, we are now
led to the view that the effect of a mass such as the Sun is to curve
spacetime, which we represent by an "embedding diagram."
We say that a flat spacetime has a Euclidean geometry. Then
the effect of a mass is to make the geometry around itself non-Euclidean.
And in a gravitational interaction everything is moving in "straight lines" in
this curved spacetime. Technical note: sometimes one uses the word geodesic instead
of saying "straight lines." |
|
Beware: the surface is a representation of the three spatial dimensions plus
the time dimension. Thus there is no physical dimension into which the surface
can be distorted. Thus, the embedding diagram is just a visualisation technique.
"So long as one believes that the universe is a big machine, it is natural
to think that its various parts can exert a force on one another. But the deeper
science probes toward reality, the more clearly it appears that the universe
it not like a machine at all. So Einstein's Law of Gravitation contains nothing
about force. It describes the behavior of objects in a gravitational field
- the planets, for example - not in terms of `attraction' but simply in terms
of the paths they follow." -- Lincoln Barnett, The Universe and Dr.
Einstein , pg. 42
This view also seems consistent with a much earlier statement of Chinese philosophy:
"The inviolability of natural laws rest on [the] principle of movement along
the lines of least resistance. These laws are not forces external to things,
but represent the harmony of movement immanent in them." -- I Ching
It is also reminiscent of a graffiti: Gravity is a myth; the Earth sucks!
"Spacetime tells mass how to move; mass tells spacetime how to curve." --
Edwin F. Taylor and John Archibald Wheeler, Exploring
Black Holes, back
cover. This well known quote from Taylor and Wheeler also appears in many
other places.
Piece 2 - Hiding the Universe in the Universe: The Principle of Equivalence
sub-section of §13.3 of the text
We all know that we can describe the gravitational interaction with:
We also know that we can describe the momentum of an object by:
Although both equations contain the mass m, a moment's reflection
may convince you that they are describing very different properties of an object.
In Eqn. D.1 we are talking about the gravitational mass, the property
that bodies have that cause them to interact gravitationally. In Eqn D.2 we
are talking about the inertial mass, the property that causes bodies
to have inertia. Why should those two very different properties of objects
have the same value?
We can compare the gravitational mass of two objects by weighing them, i.e.
measuring their gravitational interaction with the Earth. We can also compare
the inertial mass of the same two objects by measuring their effects in collisions
with other objects. These experiments have been done to great accuracy and
precision, and the ratios always come out the same for gravitational and inertial
mass. Thus we conclude that the gravitational and inertial mass are experimentally
found to be the same for all objects.
In the 19th century Mach elevated the equality of gravitational
and inertial mass into what is now called Mach's Principle. As we
shall see, although we will be able to achieve some understanding of this principle,
a complete and unambiguous statement of it is difficult, maybe even impossible.
One approach involves the Foucault Pendulum, which was invented
by Jean Bernard Foucault (pronounced foo-ko ) in 1851 in Paris
and was demonstrated for the first time at the world's fair in the Pantheon
in Paris.
The pendulum, the big brass ball in the figure, swings back and
forth. However, the plane of
the oscillation rotates as the earth turns under it. If the pendulum were
at the North Pole, the plane of oscillation would make a complete revolution
in 24 hours.
From our perspective, it seems the entire universe circles us every 24 hours.
However, the pendulum seems to show that it is the Earth that is rotating, not
the universe
|
 |
| Foucault Pendulum at the University of Louisville |
|
Newton's Laws tell us that every body will continue at rest or in uniform
motion in a straight line unless forced to change that state of motion. And
the Foucault pendulum is trying to obey that principle by rotating its plane
of oscillation as the Earth turns under it. So this is a consequence of the
inertial mass of the ball of the pendulum.
| A Flash animation of the Foucault pendulum at the North Pole is available
via the blue button to the right. It will appear in a separate tab/window. |
 |
Here is what Mach said about the Foucault pendulum:
"The universe is not twice given, with an earth at rest and an earth
in motion; but only once, with its relative motions alone determinable.
It is accordingly, not permitted us to say how things would be if the earth
did not rotate." -- The Science of Mechanics , T.J. McCormack,
trans., pg. 266.
What he is suggesting is essentially that the property of inertia of the Foucault
pendulum here is related to its gravitational interaction with the
mass of the universe there.
| A Flash animation of the Foucault pendulum and Mach's Principle is available
via the blue button to the right. It will appear in a separate tab/window. |
 |
Jay Orear stated the viewpoint of Mach's Principle nicely:
"The point of view taken here is that your head is the center of the universe
and is always at rest. Whenever you bump your head against a wall, the distant
galaxies have suddenly accelerated and exert a strong gravitational force
on your head. In order to keep your head 'at rest', the wall must exert an
equal and opposite contact force. So the next time you bump your head or
stub your toe, you can blame it on the distant galaxies." -- Fundamental
Physics 2nd
ed., pg. 288.
Incidentally, the title of this sub-section is from Chuang Tsu 6 .
Stop To Think D.1
Imagine a test mass m in a universe where there is no other mass.
Will Conservation of Momentum be true for the mass?
Piece 3 - The Equivalence Principle
The realisation that Geometry is Physics is largely attributable to Riemann
in the 19th century and Mach's Principle, also from the 19th century, is of
course due to Mach. Here we describe Einstein's insight that allowed him to
fuse Riemann's idea and Mach's Principle into the General Theory of Relativity.
Imagine that the room in which you are sitting is a cabin on a rocket ship.
The cabin has no portholes so you can not look out. Devise an experiment to
determine which of the following two situations are true:
- The rocket ship is sitting stationary on the surface of the Earth, where
the acceleration due to gravity is 9.8 meters per second per second down.
- The rocket ship is in free space accelerating upward at 9.8 meters per
second per second.
It turns out that for a reasonably small cabin on the rocket ship, no such
experiment can be devised. In 1908 Einstein elevated this to a general principle:
"We
shall therefore assume complete physical equivalence between the gravitational
field and the corresponding acceleration of the reference system. (Reference: Jahrbuch
der Radioaktivitat un Elektronik 4 (1908) pg. 443.)
We call this Einstein's
Equivalence Principle, which he later described as "the happiest thought
of my life."
Einstein once stated the principle as:
"For an observer in free fall off the roof of his house, there exists for
him during his fall no gravity."
At the very beginning of this document I stated that building a theory that
considers observers in any state of relative motion, including relative acceleration,
would also turn out to be a theory of gravitation. The Equivalence Principle
is why this is true. A few years ago a student wrote a paper which had an appropriate
typo: gravitivity.
If you think about this sub-section and the previous one, you may come to
the conclusion that the equivalence of inertial and gravitational mass is intimately
related to the equivalence of acceleration and gravitation. This conclusion
is correct, which is why Knight calls the fact that inertial and gravitational
mass are equal the "Principle of Equivalence." In these notes I make a small
distinction between these two ideas.
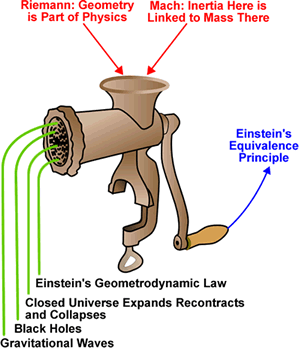
D.2 Einstein's Synthesis
The following figure neatly summarises Einstein's achievement. It is based
on a figure by J.A. Wheeler, "From Relativity to Mutability" in J. Mehra, ed., The
Physicist's Conception of Nature (Reidel, 1973), pg. 205.
You may wish to know that the General Theory, built from three elegant and
beautiful pieces, is mathematically very complex. However, the worldview that
it gives us of the nature of space and time is also elegant and beautiful.
Some chronology may be interesting here. Einstein published the Special Theory
of Relativity in 1905, based on 10 years of struggle with the question of what
he would see if he pursued a beam of light at the speed of light. He thought
of the Equivalence Principle a couple of years later, publishing it in 1908.
He did not complete and publish the General Theory of Relativity until 1915,
although he had been working hard on the problem since 1908. As he wrote to
Sommerfeld in 1912:
"I am exclusively occupied with the problem of gravitation and hope with
the help of a local mathematician friend [Marcel Grossman] to overcome all
the difficulties. One thing is certain, however, that never in life have
I been quite so tormented. A great respect for mathematics has been instilled
within me, the subtler aspects of which, in my stupidity, I regarded until
now as pure luxury."
More About Mach's Principle
According to General Relativity, in addition to the usual gravitational field
proportional to 1/r2, for accelerating masses there is
an additional field proportional to 1/r.
| Although General Relativity does not talk
about forces, we can approximate the curvature of spacetime as a force.
If two masses m and M have a relative acceleration a,
then the 1/r field
produces a force in the opposite direction to the relative acceleration
that is approximately equal to: |
 |
If we sit on a mass m that is accelerating relative to the galaxies,
the total force exerted on m
is the sum of Eqn D.3 for all the galaxies.
Assuming an average density of the matter in the universe is  and
a maximum radius R, then integrating Eqn D.4 gives:
and
a maximum radius R, then integrating Eqn D.4 gives:
As discussed below, the radius of the visible part of the universe is about
15 billion light years. As also discussed below, estimating the average density
of the universe is difficult, but perhaps a reasonable value is 10-25 kg/m3.
Then:
Thus within experimental uncertainties we have derived Newton's Second Law
from General Relativity.
Stop to Think D.2
Do you think an accelerating charge would produce an electric field proportional
to 1/r in addition to the usual inverse square field?
D.3 Predictions of General Relativity
Here we briefly describe some of the predictions of the General Theory of
Relativity and their experimental tests.
Gravitational Time Dilation
In Special Relativity moving clocks run slow. Similarly, clocks in gravitational
fields run slowly. This prediction of the theory has been tested and confirmed
many times.
Deriving Gravitational Time Dilation
Here we qualitatively derive gravitational time dilation.
The "derivation" uses Einstein's Principle of Equivalence and the idea
we first encountered in Special Relativity: the time for some event is
measured by a clock right beside where the event occurs.
We imagine we have two clocks, labeled1 and 2,
that are fixed and stationary relative to the surface of the Earth.
We are in a reference frame that is in free fall towards the surface
of the earth, and we have our own clock, stationary with respect to us.
Note that since we are in free fall, we are floating.
According to the Equivalence Principle, our reference frame is inertial,
and therefore our clock can do good measurements of time. Note that any
other clock, stationary relative to us, at some other location is not
necessarily doing good measurements of time. Thus we will compare the
rates of the Earth clocks to ours only when we pass right by them.
|
 |
When we pass by Clock 1, it is moving with respect to us. Therefore, Special
Relativity tells us that it is running slowly relative to our clock. Similarly
when we pass by Clock 2, since it is moving with respect to us it will be running
slowly compared to our clock.
But, since we are in free fall our speed with respect to the Earth and the
two Earth-bound clocks is increasing: we are accelerating down at 9.8 m/s2 relative
to the Earth. So when we pass Clock 2, its speed with respect to us is greater
than the speed of Clock 1 when we passed by it.
Thus, for us in our good inertial reference frame we conclude that Clock
2 is running more slowly than Clock 1. So the clock in the stronger gravitational
field, Clock 2, runs more slowly than the clock in the weaker gravitational
field
Global Positioning Systems
This effect is crucial in Global Positioning Systems. As you may know, there
are over two dozen GPS satellites in orbit around the Earth. Each satellite
has an extremely accurate atomic clock, and broadcasts the time as measured
by its own clock. The GPS receiver receives the signals from the satellites,
and by measuring the time delay between when the signal was sent and when it
was received calculates where it is. However, if corrections are not made for
the facts that the clocks in the satellites are moving relative to the Earth
and are in weaker gravitational fields, the position measured by the receiver
can drift by up to 11 km for every day that the satellite has been in orbit.
Stellar Aberration
We began the discussion of General Relativity by discussing the fact that
a massive object will curve the trajectory of light passing near it. Thus the
apparent position of a distant Star will be different from its real position
if the light from it passes near the Sun. This prediction of the theory has
been tested and confirmed many times.
One of the first such confirmations, by Eddington in 1919, and Einstein's
attitudes towards his theory is provided in the following account by Ilse
Rosenthal-Schneider:
"Einstein was discussing some problems with me in his study when he suddenly
interrupted his explanation and handed me a cable from the windowsill with
the words, `This may interest you.' It was the news from Eddington confirming
the deviation of light rays near the sun that had been observed during
the eclipse. I exclaimed enthusiastically, `How wonderful, this is almost
what you calculated.' He was quite unperturbed.` I knew that the theory was
correct. Did you doubt it?' When I said, `Of course not, but what would you
have said if there had not been such a confirmation?' He retorted, `Then
I would have to be sorry for dear God. The theory is correct'." --
H. Woolf, ed., Some Strangeness in the Proportion (Addison-Wesley,
1980), pg. 523.
Advance of the Perihelion
| According to classical Newtonian mechanics, the planets move in
elliptical orbits around the Sun. These orbits, in the absence of perturbations
from other planets, comets, etc., should exactly repeat themselves.
In General Relativity these ellipses do not exactly repeat. The
point of closest approach of a planet to the sun is called the perihelion,
which has the same root as periscope.
The figure shows this "advance of the perihelion" predicted by General
Relativity, although the advance is not nearly as large as the figure
indicates.
Figure source: http://astrosun.tn.cornell.edu/courses/astro201/merc_adv.htm |
 |
This prediction of General Relativity has been experimentally tested for the
orbit of Mercury. The measurements are difficult but it is probably fair to
say the prediction is confirmed.
| A Flash animation comparing Newton and Einstein's prediction of the orbit
of Mercury may be accessed via the blue button to the right. It will appear
in a separate tab/window. |
 |
Gravity Waves
Just as an oscillating electric charge generates an electromagnetic wave,
General Relativity predicts that an oscillating mass will generate a gravity
wave. Many attempts have been made to detect the existence of gravity waves,
with results that are ambiguous at best.
There are currently some experiments that are being designed to attempt to
detect these waves. One large project is the Laser Interferometer Gravitational-Wave
Observatory (LIGO). The home page of the project is http://www.ligo.caltech.edu/ .
You may wish to note that the experiment uses huge Michelson Interferometers.
Black Holes
When a gravitational field, a curvature in spacetime, becomes sufficiently
intense, the theory predicts that the matter causing the field can be literally
crushed out of existence, although the curvature of spacetime remains. The
curvature is so intense that a hole is punched in the fabric of spacetime.
This phenomenon is called a black hole.
The reason why these objects are called black holes is because at some
distance away from the central singularity the curvature of spacetime
becomes so intense that not even light can escape.
There are many observations that strongly suggest the existence of black
holes that were formed when a star exhausted its nuclear fuel. |
 |
Expanding Universe
In 1915, when Einstein was finishing up his General Theory he realised that
it predicted an expanding universe. However, the permanence of the universe
was a fixed item of Western philosophy. This conflict between a dynamic non-permanent
universe and the firm philosophical beliefs of the day bothered Einstein greatly.
In fact, he weakened and modified his theory, introducing a cosmological
constant , a fudge factor to make the universe static.
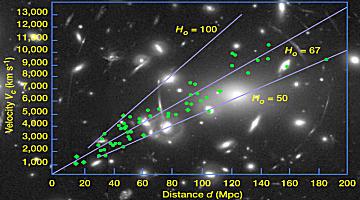
In 1929 Edwin Hubble was doing some interesting observational astronomy. It
was known that there is a class of stars called Cepheid variables whose
intensity varies periodically. Further there was a known relationship between
the absolute brightness of a Cepheid variable star and the rate of the oscillation
of its intensity. Thus by measuring the brightness of such a star on Earth
we can calculate how far away the star is.
In addition, the spectrum of the light from a star when the star is at rest
relative to us was also known. However, if the star is, say, moving away from
us the Doppler effect will cause the wavelengths of the light to be shifted
towards the red. You have probably noticed the Doppler effect when a car playing
loud music goes by you: as it approaches the sound is shifted towards shorter
wavelengths and as it recedes the sound is shifted towards longer wavelengths.
So by measuring the shift in the spectrum of light from a Cepheid variable
we can determine its speed relative to us.
When Hubble did these measurements he discovered that the stars are
moving away from us, and the further away they are the faster they
are receding from us. The figure to the right shows a more modern set
of data. |
|
Here is a model that explains how such data can arise. We imagine that we
are making raisin bread, but have misread the recipe and instead of putting
in one teaspoon of baking powder we have put in one pound! As the dough starts
to rise, it begins to fill our kitchen. If we stand on any given raisin, all
the other raisins will be receding away from us; the further away the raisin
is the faster it recedes away from us. Similarly, if the universe is expanding
and the raisins represent the stars we will get a result similar to the one observed
by Hubble.
Here is a more accurate model. We imagine the universe as a Flatland confined
to the surface of a balloon. Paint some dots on the balloon and think of them
as the stars. Begin blowing up the balloon. If you stand on any dot and measure
the position and speed of any other dot you will find that all the dots are
receding away from you and their speed away from you increases the further
away the dot is. Note that the dots are not moving on the surface of the balloon,
rather the fabric of the balloon itself is expanding. Also remember that you
must make your distance measurements staying within the surface of the balloon;
the higher-dimensional direct connection from point to point via a chord inside
the balloon is not accessible to us.
When Hubble published his results, Einstein immediately dropped the cosmological
constant, calling it "the biggest mistake of my life."
Note that the Hubble data, as well as the two models we have used to think
about it, indicate that at some time in the past the universe was very very
small. In fact, current cosmology tends to favor a view that at some time on
the order of 15 billion years ago the size of the universe was zero .
At this time, the temperature was infinite, and the Big Bang occurred,
initiating this cycle of the universe.
D.4 Problems
Until recently Big Bang cosmology was thought to be well understood. It accounted
for a great deal of data regarding the large scale structure of the universe.
Some problems were known, including:
- The flatness problem : Why is the matter density of the
universe so close to the unstable critical value between perpetual expansion
and re-collapse into a Big Crunch?
- The horizon problem : Why does the universe look the same
in all directions when it arises out of causally disconnected regions? This
problem is most acute for the very smooth cosmic microwave background radiation.
- The dark matter problem : Of what stuff is the Universe
predominantly made? Analysis of the gravitational interactions of galaxies
shows much more matter than we can see. Nucleosynthesis calculations suggest
that this dark matter of the Universe does not consist of ordinary
matter - neutrons and protons?
Then in 1998 Perlmutter et al. published data that showed that, contrary to
expectations, the rate of expansion of the universe is actually increasing.
They measured the brightness and redshift of supernovae. The brightness is
a direct measure of their distance away from us, and the redshift measures
the speed of the supernovae away from us. Thus Perlmutter was taking the same
sort of data as Hubble did 70 years before, but this time for supernova, which
are much further away from us than the Cepheid variable stars that Hubble used.
For the data to the right the upper red line is for a finite universe
whose rate of expansion is increasing. |
 |
This experiment was recently replicated by NASA, and the Perlmutter's data
was duplicated with better precision and accuracy.
This makes no sense. We expect that all the mass of the universe is gravitationally
attracting all the other mass. Thus we expect the rate of expansion of the
universe to be decreasing, not increasing. Various attempts are currently underway
to explain this mysterious result. Two of those attempts are:
- Dark Energy. This is some sort of unobservable substance
causing the rate of expansion to increase. Nobody has any idea what such
energy is. It is almost some sort of anti-gravity pushing all the masses
of the universe away from all the other masses.
- Cosmological Constant. Just as Einstein introduced a fudge
factor into General Relativity to force the universe to match his pre-conceived
idea of what the universe is like, this is a new fudge factor introduced
to force the rate of expansion of the universe to increase.
This may be a very exciting time for Physics: it is possible that the General
Theory of Relativity, time tested for over 90 years, is collapsing!
Other Animations
Here are some other animations illustrating the Theories of Relativity. They
may all be accessed via the blue button, and will open in a new tab/window.
| A Flash animation on Time Dilation in Special Relativity |
 |
| A Flash animation on Length Contraction in Special Relativity |
 |
| A Flash animation on Simultaneity in Special Relativity |
 |
Note: In the Length Contraction animation, I state that the lifetime of a
muon at rest relative to us is 2.196 us. This is the mean lifetime.
The text on page 1159 also discusses muon decay and states that the half-life is
1.5 us, which is also correct. The mean lifetime is not the same as the half-life.
The difference is not important for our purposes.
Stop To Think Answers
Stop To Think C.1
Years. Light travels a distance of one light year in a time of one year. In
this system of units, the speed of light is exactly 1 light year per year.
Stop To Think C.2
Vertical. It makes an angle of 90° with the x axis. The x coordinate of
the object does not change.
Stop To Think D.1
No. Conservation of Momentum states that the inertial mass minertial
times the speed v is constant. But according to Mach's Principle the
inertial mass is zero.
Note that in a universe with only this test mass, we and our apparatus to
measure its momentum could not exist.
Stop To Think D.2
Yes. This is the field that causes a wave of electromagnetic radiation.
Suggested Exercises and Problems
SCN 1
Assume that the speed of light is c relative to the ether. The ether
wind v is blowing horizontally towards reflector R2.at
3.00 x 104 m/s. The lengths of the arms of the interferometer are
equal, with value L = 10.0 m. Light of frequency f = 6.00
x 1014 Hz
is emitted by the source.
- Verify Equation A.1.
- When the light reaches the detector, what is the difference in phase of
the two beams?
- If the interferometer is rotated by 90 degrees, what is the difference
in phase of the two beams?
- Would the difference between your answers to Parts B and C be observable?
SCN 2
Show that the relativistic Doppler effect, Equation 20.41, is correct.
SCN 3
Relative to some observer Event 1 occurs at position x1 and
time t1.
Event 2 occurs at position x2 and time t2 where t2 is
> t1. Imagine that some signal is generated by Event
1 which arrives at the position of Event 2 just as it occurs.
The interval squared s2 defined by Equation 37.19 of the
text can be negative, zero, or positive. For each of these three cases, what
must be the speed of the signal going from Event 1 to Event 2?
SCN 4
- Show that Eqn C.7 gives a reasonable result for uLou = v,
i.e. the particle is not moving relative to the train.
- Show that Eqn C.7 gives a reasonable result for uLou =
c, i.e. the particle is moving at the same speed as the light.
- (Challenging) Assume that the speed of light is c relative to
the ether, and that Lou is stationary relative to the ether. Show that the
equivalent of Eqn C.9 is the common sense expression for the addition of
velocities.
SCN 5
Special Relativity tells us that spacetime has four dimensions, the three
spatial ones and time. Thus the relativistic equivalent of the position
vector is:
The relativistic equivalent of the magnitude squared of the position vector
is the interval squared
The value of the interval squared is invariant with the same value
in all inertial reference frames.
The textbook derives another invariant quantity, Equation 37.45, which can
be written in terms of a four dimensional vector momentum with magnitude squared
given by
What is the time component of the four dimensional vector momentum?
Solutions
Reminder: looking at solutions to problems you have not made a good try at
solving is usually not of benefit. You may see the solutions to the problems
by clicking here.
Author & Sources
These Notes were written by David M. Harrison, Dept. of Physics, Univ. of
Toronto, in February 2009.
In March 2009 PHY132S student Dylan Jacobs contributed to the discussion
of GPS systems, PHY132S student Bernard Kadosh bourght the Carl Sagan video
about Flatland and tesseracts to my attention, and PHY132S student Michael
Berg contributed to the discussion of the Foucault pendulum. In April 2009
PHY132S Learning Assistant (aka "Teaching Assistant") Omar Gamel contributed
to the discussion of the significance of the minus sign in the expression for
the interval.
Much of the material on Special Relativity is contained in a
larger non-mathemtical document I wrote in 1999:
http://www.upscale.utoronto.ca/PVB/Harrison/SpecRel/SpecRel.html.
Much of the material on General Relativity is contained in a
larger non-mathematical document I wrote in 2000:
http://www.upscale.utoronto.ca/PVB/Harrison/GenRel/GenRel.html.
The Parable of the Surveyors is from Edwin F. Taylor and John Archibald Wheeler, Spacetime
Physics (Freeman, 1966), pg. 1. This classic book is highly recommended.
Section C.6 is based on N. David Mermin, "Relativistic addition of velocities
directly from the constancy of the speed of light," American Journal of
Physics 51(12),
December 1983, pg. 1130 - 1131.
The geometric approach to addition of velocities is based on Jerzy Kocik,
"Geometric diagram for relativistic addition of velocities," American Journal
of Physics 80(8), August 2012, pg. 737 - 740..
The More About Mach's Principle sub-section is based
on Jay Orear, Fundamental Physics (John Wiley & Sons, 1967),
pg. 287 - 288.
Last revision: $Date: 2012/07/27 18:14:00 $ (y/m/d UTC).