A Mathematical Supplement - Extending the Derivation of Time Dilation
In an earlier supplement, we went through the mathematics of deriving time
dilation. We now extend that derivation to a slightly different circumstance.
In the process we shall see that in the absence of length contraction and the
fact that the speed of light is the same number for all observers, there is
no time dilation.
A New Circumstance
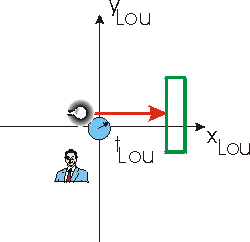
Earlier we considered Lou with a light source, light detector,
and a clock all at approximately the same physical location and stationary
relative to him. He also had a mirror stationary with respect to him,
that was located vertically above the source, detector and clock. The
figures to the right are the same ones we used earlier to show this situation.
You will recall that Sue is moving to the right relative to Lou at a
speed v. |
 |
 |
|
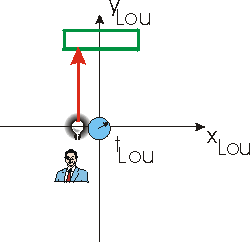
In the new circumstance the apparatus has been rotated by 90 degrees.
The figure to the immediate right shows the light travelling from the source to the mirror, and the figure to the far right shows the light travelling from the mirror to the detector. As before, the distance from the light source/detector to the mirror is
d, so the time between the emission of the light and
its detection is:
tLou = 2 d / c
which is the same result as before.
|
|
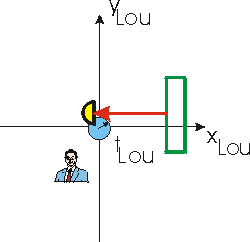 |
For Sue, the length from the source/detector to the mirror is contracted.
| |
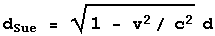 |
(1) |
The time between the emission of the light and it hitting the mirror is t1.
During this time the light will travel a distance c t1
and the mirror will travel a distance v t1. The
sum of these two distances is just the distance between the light source and
the mirror, so:
| |
dSue = c t1
+ v t1 |
|
| so: |
t1 = dSue/(c
+ v) |
(2) |
When the light leaves the mirror it "chases" the detector, which
is moving to the left at a speed v relative to Sue. The time
between the light leaving the mirror and it catching the detector is t2.
In this time the detector will travel a distance v t2 so
the light will travel a distance of dSue+ v
t2. Thus:
| |
dSue + v t2
= c t2 |
|
| so: |
t2 = dSue/(c
- v) |
(3) |
The total time between the emission of the light and it entering the detector
is t1 + t2. Combining
Equations 1, 2 and 3 gives the same time dilation factor as before:
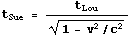
The Non-Relativistic Result
For non-relativistic speeds, three things are different than the above analysis:
- The distance between the source and the mirror is not contracted so dSue
= d.
- If the speed of the light is c relative to Lou, then when
it is travelling to the right its speed is c - v
relative to Sue. Thus Equation 2 becomes:
t1 = d / c.
- When the light is travelling to the left, its speed relative to Sue is c
+ v. Thus Equation 3 becomes:
t2 = d / c.
Thus the time between the two events, the emission of the light and it entering
the detector is just 2 d / c, exactly the
same as the time for Lou.
Acknowledgement
Thanks to Tony Reynolds, whose question prompted the creation of this supplement.