Case 1
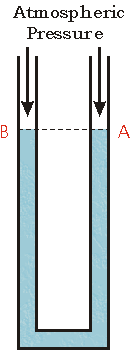
In the figure to the right we show such a U shaped tube filled with a liquid. Note that both ends of the tube are open to the atmosphere. Thus both points A and B are at atmospheric pressure. The two points also have the same vertical height.
Case 2
Now the top of the tube on the left has been closed. We imagine that there is a sample of gas in the closed end of the tube.
The right side of the tube remains open to the atmosphere. The point A, then, is at atmospheric pressure.
The point C is at the pressure of the gas in the closed end of the tube.
The point B has a pressure greater than atmospheric pressure due to the weight of the column of liquid of height h.
The point C is at the same height as B, so it has the same pressure as B. And we have already seen that this is equal to the pressure of the gas in the closed end of the tube.
Thus, in this case the pressure of the gas that is trapped in the closed end of the tube is greater than atmospheric pressure by the amount of pressure exerted by the column of liquid of height h.

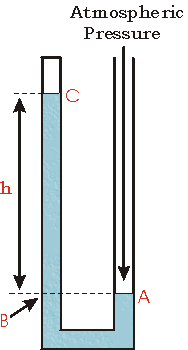
Case 3
Now we show another possible arrangement of the manometer with the top of the left side of the tube closed. Perhaps the closed end of the tube contains a sample of gas as before, or perhaps it contains a vacuum.
The point A is at atmospheric pressure.
The point C is at whatever pressure the gas in the closed end of the tube has, or if the closed end contains a vacuum the pressure is zero.
Since the point B is at the same height as point A, it must be at atmospheric pressure too. But the pressure at B is also the sum of the pressure at C plus the pressure exerted by the weight of the column of liquid of height h in the tube.
We conclude that pressure at C, then, is less than atmospheric pressure by the amount of pressure exerted by the column of liquid of height h.
If the closed end of the tube contains a vacuum, then the pressure at point C is zero, and atmospheric pressure is equal to the pressure exerted by the weight of the column of liquid of height h. In this case, the manometer can be used as a barometer to measure atmospheric pressure.