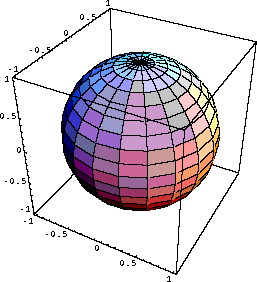Euclidean and Non-Euclidean Geometries

Click here to go the the General Relativity page.

"Geometry is the archetype of the beauty of the world." -- Kepler

Consider the following five statements about abstract classes K and L:

Any 2 members of K are contained in just one member of L.
No member of K is contained in more than two members of L.
The member of K are not all contained in a single member of L.
Any 2 members of L contain just one member of K.
No members of L contains more than two member of K.

If someone likes puzzles in logic, then various relations can be proved from the above statements. For example, it can be shown that the class K contains exactly 3 members.

We can form a model that obeys the above five statements, and then logically all relations derived from the statements will also be true for the model. One such model is that K is the vertices of a triangle, and L is the sides of that triangle.

The above deductive system is from E. Nagel and J.R. Newman, Scientific American 194, (June 1956) pg. 71.

Here is a more complicated logical system involving six abstract classes S, P, C, M, R, and A:

There is exactly one S containing two distinct P.
Every S may be extended.
Given two P's, there is one and only one C with one P a member of the R of C and the other P the M of C.
All A are equal.
Given an S and a P not a member of S, there exists one and only one S containing P which when extended has no member P' which is also a member of the original S.

Just as for the previous system, various relations between the classes can be derived from these statements. A model for which these 5 statements are usualy thought to be true is:

S = straight line
P = point
C = circle
M = centre of a circle
R = circumference of a circle
A = right angle

Now the 5 statements become just Euclid's 5 axioms of geometry:

There is exactly one straight line containing two distinct points.
Every straight line may be extended.
Given two points, there is one and only one circle with one point a member of the circumference of the circle and the other point the centre of the circle.
All right angles are equal.
Given a straight line and a point not on the line, there exists one and only one straight line through the point which is parallel to the original line.

The axioms were considered to be self-evident truths about geometry. However, the fifth axiom about parallel lines seems to some to be less simple and self-evident than the other four, and for some centuries people tried to derive the fifth axiom from the other four. A succesful derivation would prove that is was not independent and in fact not an axiom at all. The attempts all failed.

In 1817 Carl Friedrich Gauss wrote:

"I became more and more convinced that the necessity of our [Euclidean] geometry cannot be demonstrated, at least neither by, nor for, the human intellect. In some future life, perhaps, we may have other ideas about the nature of space which, at present, are inaccessible to us. Geometry, therefore, has to be ranked until such time not with arithmetic, which is of a purely aprioristic nature, but with mechanics" -- Werke 8

One of the many relations (theorems) that can be derived in Euclidean geometry is that the sum of the angles of a triangle is 180 degrees. Gauss actually did the experiment, using geodetic measurement on the top of 3 mountains: the sum of the angles came out to be 180 degrees within experimental uncertainty.

Also in the early 19th century Bolyai and Lobatchevski tried a different approach to determining whether or not the fifth Euclidean axiom is independent of the other four.

Lobatchevski changed the parallel line axiom to read:

Given a straight line and a point not on the line, there exists an infinite number of straight lines through the point parallel to the original line.

Lobatchevskian Flatland He then discovered that a logically consistent, if weird, geometry could be derived from Euclid's first four axioms plus the changed fifth one. From this he concluded that the fifth axiom really is independent of the other four; if it depended on the other statements then one would expect that the new set of axioms would show logical inconsistencies.

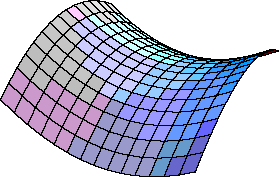
One of the relations that Lobatchevski discovered is that the sum the angles of a triangle is less than 180 degrees.

There is a model of a space in which this Lobatchevskian geometry is true: the saddle shaped plane shown to the right. In this space, for example, the sum of the angles of a triangle is less than 180 degrees. The difference from 180 degrees depends on the degree of curvature of the space: if it were almost flat the difference might not be measurable.

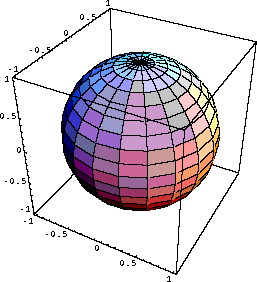Similarly, one may change the fifth axiom to read:

Given a straight line and a point not on the line, there are no straight lines through the point parallel to the original line.

In this geometry, the sum of the angles of a triangle is always greater than 180 degrees. A model is the surface of a sphere.

This geometry was developed by G.F.B. Riemann. Often his work is presented as we have done above, an exercise in logic and mathematics. However, Riemann himself always suspected, correctly as it turns out, that his geometry had something to do with the large scale structure of the universe.

If you have access to a globe, you can demonstrate Riemannian geometry. Take a piece of string and stretch it between any two points on the surface of the globe. When the string is taut, it traces the shortest distance between the two points on the surface, which means it is in some sense a straight line. Lengthen the distance between the two points and eventually the two ends of the string will meet, and will have formed a circle whose center is the center of the globe. Tape this circle to the globe. Now take another piece of string and try to construct another straight line that when extended never intersects the first string. You will quickly find that such a second parallel line does not exist. Technically, we usually call these lines geodesics.

With three pieces of string you can construct a triangle on the surface of the globe, and convince yourself that the sum of the angles of the triangle is greater than 180 degrees.