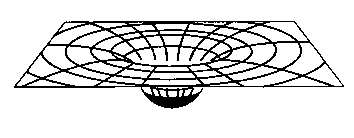
Above is the embedding diagram of a normal star. Of course, the more massive the star, the deeper the "well" in the centre.
Click here to go to the JPU200Y home page.
Click here to go to the Physics Virtual Bookshelf
Click here to go to the UPSCALE home page.
"A luminous star, of the same density as the Earth, and whose diameter should be two hundred and fifty times larger than that of the Sun, would not, in consequence of its attraction, allow any of its rays to arrive at us; it is therefore possible that the largest luminous bodies in the universe may, through this cause, be invisible." -- Pierre Laplace, The System of the World, Book 5, Chapter VI (1798).
When this "fuel" is exhausted, there are three possible outcomes, depending on the total mass of the star:
The existence of black holes is another prediction of General Relatvity, although we saw in the Introduction that Laplace made a similar prediction in 1798. Astronomers believe they have suggestive evidence that black holes exist.
Above I characterised a black hole as an object whose gravitational pressure is so intense that the matter of the object is crushed out of existence. Here is another way of characterising the same phenomenon.
 |
|
Above is the embedding diagram of a normal star. Of course, the more massive the star, the deeper the "well" in the centre. |
 |
|
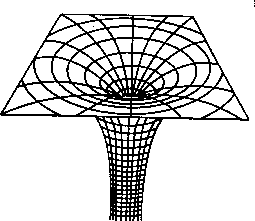
Here is the embedding diagram of a black hole. The gravitation is so intense that it has punched a hole in the fabric of spacetime. We call the hole in spacetime a singularity. |
| Einstein did not like the singularity in the centre of the black hole. In 1935 he and Rosen found another solution to the equations of a black hole. It is shown to the above. There is an Einstein-Rosen bridge or wormhole connecting two different regions of spacetime. | 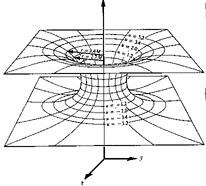 |
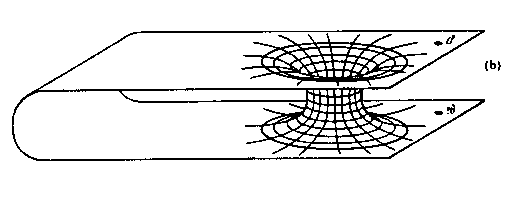 |
| The Einstein-Rosen solution does not say anything about the relationship between the two regions of spacetime. One possibility is shown above. The black hole in some region of spacetime connects to a black hole in another region of spacetime. |
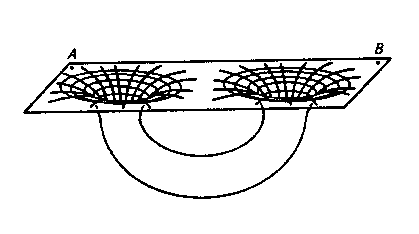 |
| The previous figure can be a bit mis-leading in trying to interpret distances. Here is a topologically equivalent version of the first one. |
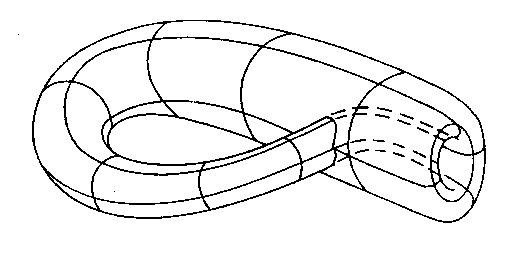 |
| Finally, a sort of wild speculation. The Klein bottle shown above may be a model for how a black hole in the universe can connect to the universe as a whole. |
 |
| Above we have a star, and have drawn the path of light rays being emitted from a point on the surface. As we know, the light will be attracted by the mass of the star. For rays that are emitted nearly parallel to the surface of the star, they will end up falling back to the surface of the star. We have drawn an exit cone; light emitted inside the cone escapes from the star, and light emitted outside the cone falls back to the star. |
| Now we have a more massive star. As we see, the exit cone is now smaller. |  |
For a black hole, there is a point at some distance away from the center where the gravitation is so strong that the exit cone totally closes. Thus, nothing closer to the center than this can ever escape. This is why we call these objects black holes.
The distance from the center for which the exit cone closes is called the Schwarzschild radius. The sphere surrounding the singularity of this size is called the event horizon since no events that happen inside it can ever be known to us.
 The figure shows the spacetime diagram of an object
falling into a black hole. As measured with our rods and clocks we see that it
takes an infinite length of time for the object to cross the event horizon at x
= 2. Coming out of the mathematics of General Relativity is the worldline of
the object inside the event horizon: apparantly it crosses the event horizon at
time t = infinity, and then travels backwards in time to finally crash into the
singularity at time t = 44.
The figure shows the spacetime diagram of an object
falling into a black hole. As measured with our rods and clocks we see that it
takes an infinite length of time for the object to cross the event horizon at x
= 2. Coming out of the mathematics of General Relativity is the worldline of
the object inside the event horizon: apparantly it crosses the event horizon at
time t = infinity, and then travels backwards in time to finally crash into the
singularity at time t = 44.
The figure also includes the light cones of the object. We see that as the object approaches the event horizon, the light cone closes up. This should remind you of the exit cones we discussed above.
You can also see that inside the event horizon the light cones are now about a horizontal axis instead of a vertical one. Here is one way of thinking about this. Out here, we are free to move in any direction we wish in space. However, we can not choose in what direction to go in time: we are constrained to always get older, not younger. Inside the event horizon the object is constrained to fall into the singularity; it has no freedom of movement in space. Whether this means that it has some sort of freedom in time is a good question which I do not know how to answer.
If we are riding with the object as it falls into the black hole, we would not experience the infinite time dilation shown in the spacetime diagram: we would just fall through the event horizon. However, if we are falling, say, feet first the gravitational "pull" on our feet is stronger than on our head since it is closer to the singularity. This tidal force is sure to rip us to bits long before we actually get to the event horizon.
Reference for the figure: Misner, Thorne and Wheeler, Gravitation, pg. 848.
We can calculate the Schwarzschild radius for the mass of the Earth: it works out to be about one-third of an inch. What this means is that if we could compact the Earth so that its radius gets down to one-third of an inch, the gravitational attraction becomes strong enough that the Earth gets crushed out of existence, creating a black hole.
The comparable figure for the mass of the Sun is about 1.1 kilometers.
For a mass of 2.5 x 1053 kg, i.e. a 2 and a 5 followed by 52 zeroes kg, the Schwarzschild radius is about 17 billion light years. This huge mass is an estimate for the total mass of the universe. Also, given that the age of the universe is 15 billion years or so, 17 billion light years is awfully close to the size of the universe. Does this mean that the universe itself is a black hole?
It turns out that this question is the same as asking: is the universe closed. If the universe is closed, then it is fairly accurate to say that it is a black hole.
This document is Copyright © 1999, 2000 David M. Harrison. This is version 1.5, date (m/d/y) 02/06/02.
i was considering how
within night's loose
sack a star's
nibbling in-fin
-i-
tes-
i
-mal-
ly devoursdarkness the
hungry star
which
will e
.
-ven
tu-
al
-ly jiggle
the bait of
dawn and be jerkedinto
eternity. when over my head a
shooting
star
Burs
(t into a stale shriek
like an alarm-clock)
-- e.e. cummings
(Note: the spacing of the above poem is not rendered quite correctly by the Internet Explorer browser.)