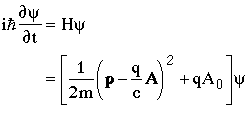
PHY357S: Monday, 30 March 1998

Answer 1

The mass difference between the X^- and X⁰ baryon is only 1321.32-1314.9=6.4MeV, so the only X^- -> X⁰X^- decay which conserves energy, electric charge, lepton number, etc. is X^- -> X⁰e^-(antin_e). The X^- and X⁰ both have the same strangeness and are isospin I=¹/₂ partners, so this is just a normal beta decay just like n -> pe^-(antin_e). The decay rate should just be related by Q⁵ to the rate for neutron decay, so we expect the X^- -> X⁰e^-(antin_e) decay rate to be just (6.4/1.293)⁵(1/896s)=(1/0.30s). The lifetime of the X^- is 1.636x10^-10s, so the branching ratio is 6x10^-10. This is too small a rate to have ever been observed.

Answer 2

Starting with the Schrödinger equation (F&H Eqn. 7.1) and the electromagnetic Hamiltonian (F&H Eqn. 12.1) we have

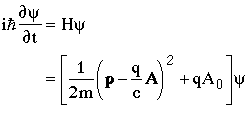
Applying the local U(1) gauge transformations (F&H Eqns. 12.2 & 12.3) we have:

Left-Hand Side

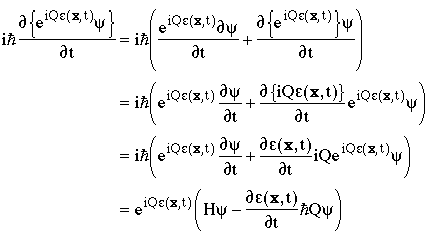
Right-Hand Side

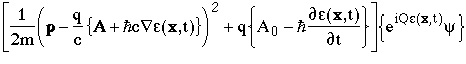
Substituting in the momentum operator

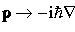
(e.g. F&H Eqn. 14.25 ) gives

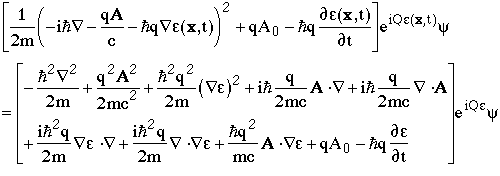
where we have dropped the explicit notation e(x,t) in order to save space (but we must not forget that e depends on x & t). Now

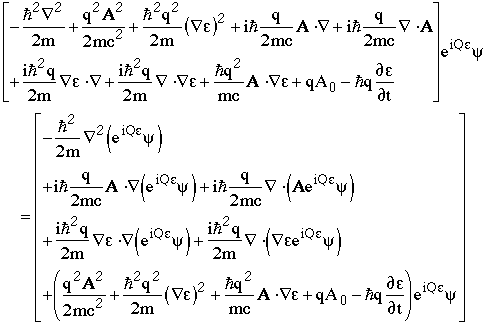
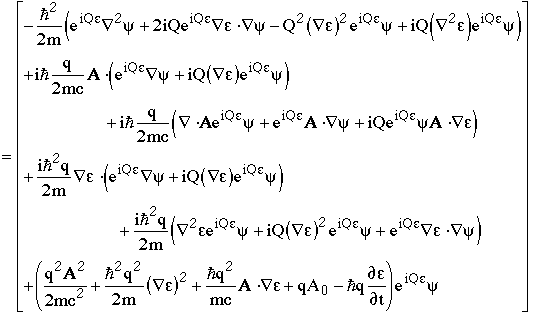
Now factor out the exponential term and expand

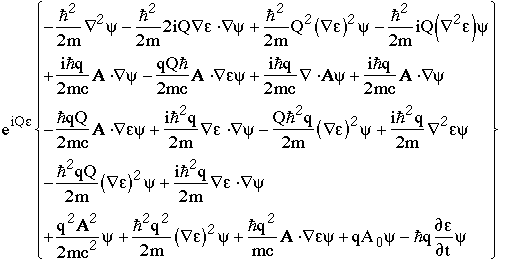
and gather together common terms

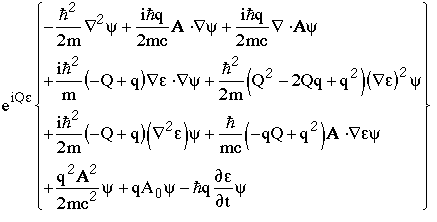
At this point I remember that Q is actually the charge operator, Qy=qy, so we see that almost all the "e" terms vanish

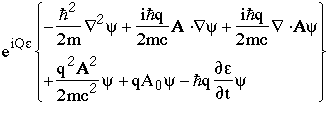
Gathering the quadratic terms and sticking back in the p and e(x,t) notation gives

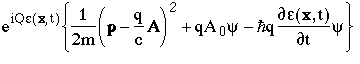
which immediately gives the left-hand side, as required.

which immediately gives the left-hand side, as required.

Answer 3

The neutrinos produced by pion decays are almost 100% muon neutrinos (See F&H Table A3), but then the muons also decay into muon and electron neutrinos. Since I was a bit vague about how the beam was produced, there are several reasonable possibilities for the initial neutrino flux. e.g. If you included the neutrinos from the decays of the secondary muons, and assumed a pure p⁺ beam then the initial neutrino ratios would be (muon neutrino):(muon antineutrino):(electron neutrino): (electron antineutrino)=1:1:1:0.

The probability of a muon neutrino oscillating into an electron neutrino (or vice versa) after a time t is (see F&H Section 11.10)

The neutrinos are known (see Table A3) to be light compared to their momentum of 10 GeV, so their velocity is c and the oscillation probability after travelling a distance L is

In this case Dm²= m_nm²-m_ne² = (0.0025 eV)² = 6.25x10^-6eV² and q=p/4 so

For L=9.92x10⁵km we have

So the beam neutrinos have half oscillated into the other type.

Inside the electron ball, the neutrinos can interact with the electrons with a cross section (F&H Eqns. 13.42-13.44) for muon neutrinos of

and for

The electron density in the electron ball is

So the neutrino interaction lengths are

and for

At this point point it becomes apparent I made a small typo in the mass of the electron ball. Essentially what I did was to mix up the number of electrons in the electron ball with its mass , which increases the mass by 9.109x10³¹. (6x10⁵⁵kg mass is a couple of orders of magnitude larger than the mass of the observable universe.)

Because of my typo, clearly no neutrinos are going to come out the other side of the neutrino ball. If any did come out, however, they would be mostly muon neutrinos and antineutrinos, since the interaction lengths for both types of electron neutrinos are much shorter. (The exact values depend on what you assumed for the initial neutrino composition; you just attenuate each component exponentially using the appropriate interaction length.)

Answer 4

(a) Figure 14.1 shows us that the np cross section falls to 40mb at about 1 GeV and is then flat. A flat cross section is what we expect for billiard ball scattering with s=4pR² (see Lecture 7), so in this case R=(40mb/4p)^1/2=0.6fm.

(b) Ignoring the factors of hbar and c, substituting 14.24 into 14.22, and using the result given in Footnote 12, we have

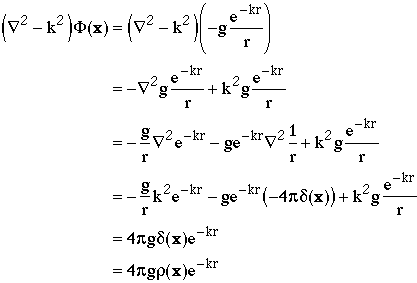
Where r(x)=d(x) is the charge density for a point particle.