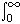PHY357S: Thursday, 12 February 1998

Answer 1

(a) The magnetic moment of a particle with absolute charge Q and mass m is

A strange quark is a point fermion with an electric charge -1/3e , so J=1/2, g=2 and Q=e/3. The nuclear magneton is m_N=e/2m_p (F&H Sect. 5.2), so

(b) The b quark effective mass is dominated by its intrinsic mass (~4 GeV from F&H Table 5.7) which much larger than the strong interaction effects which make the strange quark (and the up and down quarks) effective masses much heavier than their intrinsic masses (F&H Sect. 6.7 and Lecture 7). Since the L_b is just like the L_s, we expect its magnetic moment to be dominated by the b quark with m_beff=4GeV. Quarks are charged fermions, so

There are various ways to get this answer into eV/Tesla.. From the Lorentz force law we can see that V/m=(m/s)T, so Tesla = V·s/m² = V(3x10⁸/m) = V(3x10⁸·197x10^-9eV) = 59 V eV

An even simpler way to make the conversion is to take the value of the nuclear magneton, m_N=3.2x10^-18MeV/G from F&H, so e/2m_p=3.2x10^-8eV/T

Answer 2

The integrated flux of supernova neutrinos per unit area at the earth would be

where R is the distance from the earth to the supernova. The number of nucleons per unit mass in normal matter is about

where the atomic mass unit u=931.494 MeV=1.66x10^-27kg (from F&H Table A2) is the typical mass of a nucleon in matter. In order for the aborbed dose from neutrino interactions to be less than 10 Gray (= 10 J/kg, from Lecture 5), we must have

This is less than the distance from the earth to the sun, so although a solar supernova would finish us off, it wouldn't be the neutrinos doing it. (It has, nevertheless, been suggested that supernovae neutrinos could cause mass extinctions on earth, see the paper by J. I. Collar, Physical Review Letters 76 (1996) 999-1002. For an example of why many people are skeptical of Collar's conclusions, look at Dave Wark's comments )

Answer 3

(a) Inserting this potential into F&H Eqn. 6.14 gives

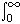f(q²)=(-2m/q) dx x sin(qx) (Z₁Ze²R/x²)

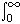\ f(q²) = (-2mZ₁Ze²R/q)d(qx) sin(qx)/(qx)

Using 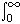dx sin(x)/x = p/2,

(b) With this charge density, we expect to see a Coulomb's law 1/r potential for r>10fm, so we expect to see the differential cross section change from 1/q² to 1/q⁴ as q²decreases below (200 MeV fm / 10fm)² = 400 MeV². So we need scattering data in the range from q²=10 MeV² to 10 GeV² or so.

(c) From F&H Section 6.10 we learn that the deep inelastic scattering cross section is obtained by averaging the square of the charge of the quarks in a nucleon. For a proton this is [(2/3)²+(2/3)²+(1/3)²]e²/3=(1/3)e²; for a neutron it is [(2/3)²+(1/3)²+(1/3)²]e²/3=(2/9)e². Hence the ratio of cross sections for helium (2 neutrons+2 protons) compared to hydrogen (1 proton) is

This estimate is not quite right because about 10% of a nucleon is actually composed of virtual quark-antiquark pairs which also contribute equally to proton and neutron scattering.

Answer 4

(a) Forbidden by lepton and muon number conservation. (The n_m has opposite lepton and muon number from a m⁺.)

(b) Allowed and will proceed by the electromagnetic interaction. (Electrons and positrons don't interact by the strong interaction.)

(c) Allowed and will proceed by the strong interaction.

(d) Allowed and will proceed by the weak interaction since there is a change of one unit of strangenss.

(e) Forbidden by baryon number conservation. (The initial state has 40 baryons, the final state 41.)

(f) Forbidden by electric charge conservation. (The initial charge is +1, the final charge is +2.)

(g) Allowed and will proceed by the weak interaction if the neutrino has just the right resonant energy.

(h) Forbidden by energy conservation. K⁴⁰ decays into Ca⁴⁰ (see Lecture 5); it is heavier and so a neutrino capture reaction can only produce an excited state of Ca⁴⁰, or the excess energy must be radiated away by a gamma ray.