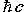PHY357S: Thursday, 30 January 1998

Answer 1

(a) Using Coulombs law (in SI form), the electrostatic force is:

where -e is the proton charge, and r = 1fm is their separation. At some point we are going to have to do some unit conversions, so Tables A1 and A2 in F&H are helpful. As it happens, a=e²/(4pe_{0 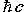)} is just the fine structure constant 1/137.0360, so we have

(b) From Tables A2 and A3 we have the proton, deuteron, and neutron masses to be m_p=938.272 MeV/c², m_d=1875.613 MeV/c², and m_n=939.566 MeV/c²; so the binding energy of the deuteron is DE= m_dc²-m_pc²-m_nc²=-2.225MeV. Using DE=F·dx, we can estimate that the stron force is roughly

So the strong force between two nucleons is comparable to the electromagnetic force in this case.

(Comment: This is a large part of the explanation why two protons don't form a stable bound state. We will learn later that the apparent weakness of the strong force in this case is because it is a "Van der Waal's" residual strong force between colour neutral composite objects.)

Answer 2

(a) Using F&H Eqn. 2.31 we have:

(b) For symmetric colliding beams, each beam must just have half the total energy, i.e.

(Comment: The highest energy current experiment reaches W=2 TeV at the Fermilab Tevatron; the Large Hadron Collider at CERN will reach W=14 TeV in about 10 years.)

(c) In F&H Section 2.3, the SLAC linac's parameters are given to be 20 GeV over 3 km. So to reach 700 TeV, it would have to be

(Comment: The linac has been upgraded in recent years to 50 GeV over 3km, so the extrapolated length would be only 40,000km.)

(d) The radius of the earth is about 6000km, so any accelerator that goes around the earth must have a maximum radius of curvature of about 6000km. We need to check this will cause a problem. The two obvious questions are whether this bend will be too strong for the magnets or whether there will be too much synchrotron radiation.

Since Fermilab reaches 1 TeV with a radius of curvature of 1km, reaching 700 TeV with a radius of 6000km is not a problem for the bending magnets.

F&H Eqn. 2.22 gives the energy lost by synchrotron radiation per revolution in Gaussian form. (All electromagnetic formula in F&H are in Gaussian units, see F&H Section 1.2.) From F&H Table A2 we have e=4.803x10^-10esu and m=0.510999 MeV for electrons, and 1eV=1.602177x10^-12ergs, so

and the energy loss per distance travelled is

and for E=700TeV, R=40000km/2p=6.4x10⁸cm, we have

Since the accelerator has only accelerates particles at 20GeV/3km = 6.7 GeV/km, there is no way it can replace such huge energy losses, so there is no way the electrons are going to reach 700 TeV. The maximum electron energy will be the energy where the synchrotron radiation losses just balance the the acceleration, i.e.

So it will not be possible to accelerate electrons much beyond 10 TeV by any accelerator on earth.

Answer 3

For a given substance, the Bethe-Bloch equation (F&H Eqn. 3.2) tells that the ionization energy losses of a charged particle depend just on its velocity and its charge. A 16 GeV proton has b~1 and is about minimum ionizing (see, for example, F&H Fig. 3.5), so its ionization energy losses are of the order of 2 MeV/(g/cm²) (from F&H Eqn. 3.3).

A 16 GeV alpha particle (a ⁴He nucleus) has four times the mass of a proton, so its speed will be the about the same as a 4 GeV/c proton. A 4 GeV/c proton is about minimum ionizing. An a particle has twice the charge of a proton, however, so its ionization energy losses will be four times that of the proton, i.e. about 8 MeV/(g/cm²).

The density of air (from F&H Table 3.1) is 0.0012 g/cm³, so the ionization energy loss of the proton in 2.5cm of air will be

The energy needed for production of an ion pair in air is 34eV (see F&H Section 4.3), so the average number of ion pairs produced by a proton will be

and the average number of ion pairs produced by an alpha particle will be

The detector's efficiency is 14%, so the average number of ion pairs detected are

The standard deviations are just the square root of the mean number (see F&H Section 4.2), so

For a proton to produce a 100 ion pairs would be about a (100-25)/5 = 15 standard deviation fluctuation, and for an alpha to produce 25 ion pairs would be about a (25-100)/10 = -7.5 standard deviation fluctuation.

So the detector can do a good job of telling whether the particle is a proton or an alpha.

Answer 4

Since the bubble chamber is full of hydrogen, the initial p^- can only interact with either a proton, an electron, or a deuteron. (Hydrogen has very small fraction of deuterium.) Since the net charge of the interaction's products is zero, however, the pion must have interacted with a proton. So this interaction is similar to that discussed in F&H Fig. 5.21 and Eqn. 5.54, but only one decay is observed instead of two. There must however be a second invisible neutral particle or else momentum will obviously not be conserved (since the observed neutral particle goes backward.)

Let the direction of the initial pion define the x direction, so it momentum is

(Since everything is in the plane of the paper we can ignore the z coordinate.) The charge pion mass is 139.6MeV/c² (from F&H Tables 5.5 or A3), so the intial pion's energy is (by F&H Eqn. 1.2)

The proton mass is 938.3MeV/c² (from F&H Tables 5.6 or A3) and it was at rest, so the target proton's momentum and energy are

According to my ruler (a 30 year old wooden one, yours may differ) the diameter of both secondary pion tracks is 13.5±0.1cm. The length of the "60cm" scale line is 9.98±0.1cm, so the radius of curvature of the secondary pion tracks is

(My 0.1cm measurement error is an estimate of the combined reading and repoduction distortion errors. Any common scale errors in my ruler will cancel out.)

The Argonne bubble chamber has a magnetic field of "about 18kG" (from F&H Section 4.4). The word "about" would suggest that B=18±0.5kG, so we can calculate the momentum of the secondary pions (using F&H Eqn. 2.15a) to be

and

Using the angles in the diagram, the vector momenta of the secondary pions are

The energy and momentum of the two pion system are

and invariant mass of the two pion system is(using F&H Eqn. 2.29)

To get an idea of the uncertainty, I'll just calculate this mass for p_p = 219.1+7 = 226.1 MeV/c and p_p=219.1-7 = 212.1 MeV/c, which give M_pp = 508 and 487 MeV/c² respectively, i.e. The mass of the observed secondary particle is

The second secondary neutral particle is not seen, but we can calculate its mass by subtracting the secondary neutral partcle we see from the initial system. i.e. We can calculate the "missing mass" (e.g. se F&H Problem 5.13). The missing mass is

where

Trying again p_p=224.4 MeV/c and p_p=210.4 MeV/c, I get M_misss = 1153 and 1224 MeV/c² respectively, i.e.

(a) So the masses of the two secondary neutral particles are 498±11 and 1189±35 MeV/c².

(b) The only neutral particle in Tables A3, A4, and A5 which has a mass of 498±11 MeV/c² is the K⁰. (The next closest particle is the h at 549 MeV/c², but this is several standard deviations away and does not decay into two pions.)

The only neutral particles in Tables A3, A4, and A5 which have a mass of 1198±35 MeV/c² is the S⁰ and the D⁰(1232). The S⁰ is slightly favoured since the D is about a standard deviation away in mass. If it is a S⁰, then it decays into Lg, and if the L decays into a neutron and a neutral pion it will probably be invisible, since the neutron and the two photons from the p⁰ leave no tracks and probably won't interact. If it is a D⁰(1232), then it will be invisible if it also decays in np⁰.

(Comment: Later in the course we will be learning about strangeness and baryon number conservation which provide significant constraints in this event. The second neutral particle in this case is not a D⁰(1232), since this would violate strangeness in the strong interaction between the initial pion and the target proton. So the actual interaction is p^-pÞS⁰K⁰, very similar to F&H Eqn. 5.54.)