PHY357S:
Answers to Problem Set 3
(a) Allowed, proceeds through strong interaction since all particles involved are hadrons. It can also proceed through the electromagnetic and weak interactions, but much more weakly.
(b) Allowed, proceeds through strong interaction since all particles involved are hadrons. It can also proceed through the electromagnetic and weak interactions, but much more weakly.
(c) Allowed, proceeds through weak interaction since strangeness is not conserved.
(d) Forbidden, baryon number is not conserved.
(e) Allowed, proceeds through weak interaction since neutrinos only interact weakly.
(f) Forbidden, electron and muon number are not conserved.
(g) Forbidden, electron number is not conserved (ne couples to e-, not e+).
(h) Allowed, proceeds through
weak interaction since neutrinos only
interact weakly.
(a) The electron and the antineutrino are both spin-1/2
fermions, and the inital and final nuclear spins differ by 1 unit
of angular momentum. Angular momentum is coserved
if there is no orbital angular momentum and the
antineutrino and electron spins are both aligned to the spin of
the original nucleus. Figure 9.6 shows us that the electron
prefers to come off in the direction opposite to the applied magnetic
field. The spin of a nucleus is aligned to its magnetic moment,
and the magnetic field aligns the magnetic moments, so the
electron prefers to be emitted opposite to the direction of the
nuclear spin. This means that the electron is left handed
(i.e. have negative helicity) since the electron spin is in the
same direction as the nuclear spin. From Figure 7.2 we know that
the antineutrino is always right handed
(i.e. positive helicity). If the antineutrino is usually emitted
in the same direction as the electron, then it would also have
to be left handed by angular momentum conservation. If the
antineutrino is emitted in the same direction as the nuclear spin,
then it can be right handed while conserving angular momentum.
So the electron and and antineutrino are predominantly
emitted in opposite directions.
Frauenfelder & Henley equations 12.9 includes 12.6 as the mg=0 limit. Combining 12.9 and 12.6 we have
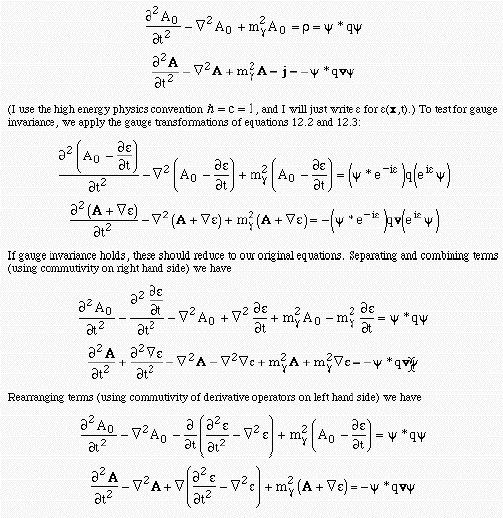Applying equation 12.8 gives us
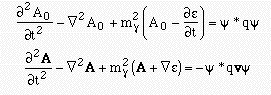
This only reduces back to equations 12.9 if _e/_t=-e=0, which corresponds to e=constant, i.e. just global gauge invariance, not local gauge invariance.
It does, however, reduce back to equations 12.6 if mg=0, so equations 12.6 are gauge invariant.
It is interesting to note that equation 12.8 is just a wave equation
corresponding e propagating at the
speed of light, so gauge invariance requires the the physical
photon field and the unphysical gauge field be massless.