PHY357S: Wednesday, 22 January 1997

Problem Set 2

due Monday, 10 February 1997

These questions are based on the lectures and on Chapters 1-6 + Appendices of Frauenfelder and Henley.
If you have any questions about these problems, ask me - preferably before the evening of 4 February. You can contact me at dbailey@physics.utoronto.ca, Room 919, or at 978-4993.

Each problem is of equal weight, but not all problems may be marked.

Problem 1

Imagine W- bosons decaying at rest into a neutron and an antiproton inside a large block of iron.The cross section for neutron-nucleus interactions is more-or-less proportional to the physical area of the nucleus, so neutron-nucleus cross sections roughly scale as A2/3, where A is the atomic number of the nucleus. (The volume of a nucleus is essentially the volume of its constituent nuclei.) The total cross section for neutron-proton scattering is shown in F&H Figure 14.1. (a) What is the mean distance a neutron will travel before it interacts hadronically with an iron nuclei? (b) Space and momentum are related to each other the same way that time and energy are, so just as finite lifetimes correspond to energy widths, finite interaction lengths should correspond to momentum widths.What is the intrinsic FWHM spread in the neutrons' momenta due to fact that they do not propagate forever through the iron.

Problem 2

The origin of the spin of the proton (uud) and neutron (ddu) is currently controversial. The quarks have zero orbital angular momentum, and most naive model is that each of the 3 quarks has its spin parallel to the nucleon spin 2/3 of the time, and antiparallel 1/3 of the time. Use the values of F&H equation 6.49 to estimate the masses of (a) up quarks and (b) down quarks.

Problem 3

Show that if the classical non-relativistic Rutherford cross section (F&H equation 6.17) is applied to ionizing collisions between charged particles and atomic electrons, the ionization energy loss formula is

This is half the nonrelativistic (bÆ0) limit of the Bethe-Bloch equation (F&H equation 3.2). The difference is because either (a) I've made a mistake, or (b) the classical minimum energy transfer(DEminªI) is much larger than the quantum statistical average minimum ().

Problem 4

The relativistic limit of F&H equation 6.13 is obtained by replacing the mass "m" by energy "E". (e.g. compare equations 6.17 and 6.19.). Consider the Yukawa potential,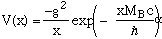, mediated between two particles of charge "g" by an intermediate vector boson of mass MB. What is the total cross section for elastic scattering of one particle (mass m1, charge g, energy E1>>m1) from the second particle (mass m2, charge g, energy E2= m2) in the limit where m1, m2<< E1<<MB2/(2m2)?