Þdecay
(pp- or np0)

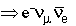
| Particle (mass)JPC
Þdecay | ||||
| r0 (769)1-- | ||||
| Þ p+p- | ||||
| Þ p+p-g | ~a | |||
| Þ e+e- | ~a2 EM (electromagnetic) | |||
| Þ g | momentum | |||
| Þ p0p0 | Bose-Einstein (BE) statistics | |||
| Þ gg | Landau-Yang theorem (BE, J) | |||
| p0 (135)0-+ | lightest hadron | |||
| Þ gg | ~a2 EM | |||
| Þ e+e-g | ~a3 EM | |||
| Þ e+e-e+e- | ~a4 EM | |||
| Þ e+e- | ~a4 EM (Note) | |||
| Þ ggg | ~a3 (C) | |||
| D0(1232)3/2+ | ||||
| Þ Np
(pp- or np0) | ||||
| N0(1440)1/2+ | ||||
| Þ Np | ||||
| Þ Npp | ||||
| n (940)1/2+ | ||||
| Þ pp- | energy | |||
| Þ pe- | J (angular momentum) & L | |||
| Þ p+e- | <2 x 10-55eV | Baryon number (B) & lepton number (L) | ||

| weak | |||
| p (938)1/2+ | lightest baryon | |||
| Þ p0e+ | B & L | |||
| d (np)1+ | ||||
| Þ p0r+ | B | |||
| p- Þ e-ne | L | |||
| L (1115) | weak | |||
| Þ Np | strangeness (S) | |||
| K+ (494)0- | weak | |||
| Þp+p0 | S | |||
| Þ m+nm | S | |||
| m- (106)1/2 | ||||
| Þ e-g | muon number (Lm) and electron number (Le) | |||
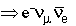
| weak | |||
| e- (0.511)1/2 | ||||
| Þ neg | electric charge (Q) | |||
| h (547) | ||||
| Þp+p- | Parity (P) & CP | |||
| Þp+p-p0 | EM (G-parity: isospin(I)+C) | |||
| Þgg | electromagnetic (EM) | |||
| p0Þ ggg | ~a3 charge conjugation (C) | |||
| p+ (140)0- | lightest charged hadron and charged boson | |||
| Þ m+nm | weak | |||
| Þ e+ne | helicity | |||
| K0L (498)0- | ||||
| Þp+p- | CP | |||
| Þp+ p- p0 |
Decay Width : Because of Heisenberg uncertainty principle, any particle with a finite lifetime has a mass distribution of non-zero width. The total decay width (G=h/2pt) is the Full Width at Half Maximum of the mass distribution. Each decay channel contributes to the total width, and the partial decay width (Gi = G · BR) is the contribution to the total width due to a specific final state. (Return)
Decay Fraction : Decay branching fraction or branching ratio (BR) is the probability of a particle decaying into a specific final state. The sum of the branching ratios should add up to 100%. (Sometimes "branching ratio" refers to a ratio of branching fractions, but in particle physics "branching ratio" is usually synonymous with "branching fraction".) (Return)
p0 Þ e+e- : Mediated by 2 virtual photons, not 1, since the pion has spin-0. The decay is also suppressed by an helicity factor of (me/mp)2. ( Return)
Helicity : Helicity is the normalized projection of a particle's spin on to its momentum, i.e. J·p/J·p. Helicity is not a relativisticly invariant quantity since momentum is frame dependent, but helicity is conserved to the extent that the probability of the helicity remaining the same is typically b=v/c. (Note: This is true independent of whether parity is conserverd.) (Return)
Strangeness (S), muon number (Lm), and electron number (Le) are examples of a "flavour" quantum numbers. These conservation laws are simply a reflection of the existence of the fundamental fermions.
The strong and electromagnetic interactions conserve the fermion flavours, e.g. the only way to get rid of an electron is to annihilate it with an anti-electron (a positron). Similarly, the only way for strong or electromagnetic interactions to get rid of a strange quark is to annihilate it with an anti-strange quark. In this sense we actually have 12 conservation laws, but some are of little importance (i.e. neutrinos don't interact strongly or electromagnetically) or are obscured by other symmetries.
Weak interactions can transform any "up" type quark (u, c, or t) into any "down" type quark (d, s, b), and vice versa, but "up" or "down" type quarks don't mix among themselves. The relative probabilities depend on the transistion. Weak interactions may also not conserve lepton flavours in a similar manner, but the experimental evidence for such transitions is not yet compelling.
Isospin symmetry is invariance under the interchange of u and d quarks. In nuclear physics, this corresponds to invariance under the interchange of protons and neutrons. In analogy to the two spin states of a fermion, up quarks (or protons) are considered to be the I3=+1/2 state, and down quarks (or neutrons) are considered to the the I3=-1/2 state. Mesons (quark-antiquark hadrons) made from u & d quarks can have isospin 0 or 1; u & d quark baryons (qqq states) can have isopin 1/2 or 3/2; nuclei can have I=0, 1/2, 1, 3/2 …
This symmetry is because u and d quarks have negligible mass compared to their strong binding energies in any hadron. As a result, replacing an up quark with a down quark makes almost no difference. For example, a proton (uud) is essentially the same as a neutron (udd), except for a tiny mass difference (~0.1%) and their electric charges.
Isospin symmetry is an accident, since there is no obvious reason why the up and down quarks should have the masses they do, but it is very powerful in understanding hadronic systems and their interactions. The symmetry is not exact, since u and d quarks do have slightly different masses and very different electric charges.
Isospin (I) is conserved by strong interactions. I3 is conserved by both strong and electromagnetic interactions, since the net number of u quarks and and the net number d quarks never changes. Isospin is a mixture of u & d flavour symmetry with the consequences of u & d quark mass degeneracy.
Sometimes both isospin invariance and charge conjugation invariance cannot both be true; this consistancy can be parameterized using the G-parity quantum number. G corresponds to making a parity transformation in isospin space giving a factor (-1)I, followed by a C transformation. G is conserved by strong interactions, since both I and C are conserved, but not by weak or electromagnetic interactions.
There are two obvious space transformations: translation (xÆx+dx) and reflection (xÆ-x). Translation is a continuous operation, but reflection is discrete - it is impossible to reflect by an infinitesimal amount.
The reflection operation is known as the parity operator, i.e.
In general, the parity operator reverses all 3-vectors, e.g.
but not axial-vectors, e.g.
Spherical harmonics (F&H Table A8) are the eigenfunctions of the orbital angular momentum operators and have parity
If y(x) is an eigenfunction of parity, then
where the eigenvalues of the observable are P=±1 because
If parity is conserved, then the parity of a system is the product of the parity of its components.
In general,discrete symmetries lead to multiplicative conserved quantitites.
Strong and electromagnetic interactions conserve P (e.g. hÞp+p- is forbidden); weak interactions do not conserve P.
In the early 1950's, two strange particle decays were observed
Pions are eigenstates of parity with intrinsic spinParity
The parity of two pions (p1 & p2) with relative orbital angular momentum L(1,2) is
| = P(p1) x P(p2) x (-1)L(1,2) | |
| = (-1) x (-1) x (-1)L(1,2) | |
| = (-1)L(1,2) |
The parity of three pions is
| = [P(p1) x P(p2) x (-1)L(1,2)] x P(p3) x (-1)L(12,3) | |
| = - (-1)L(1,2) x (-1)L(12,3) | |
| = - (-1)L(1,2)+ L(12,3) |
where L(12,3) is the orbital angular momentum between the third pion and the first two. If J is the spin of the parent particle, then by angular momentum conservation, we must have
If parity is conserved in the decay, the parity of the parent particle is the same as the parity of the final state pion system. So we expect
So the q+ and t+ cannot have the same spinparity (JP) if parity is conserved, and the q+ and t+ must be different particles.
The existence of two new particles would not be of concern except that the q+ and t+ appeared to be otherwise identical - they had the same masses, the same lifetimes, and were produced and interacted with the same lifetimes.
Further measurements showed that J(q+) = J(t+) = 0.
Why would there be two identical particles differing only by their parity?
In 1956 T. D. Lee and C. N. Yang pointed out that parity conservation had never been tested for the weak interaction. If parity was not conserved, the q+ and t+ were simply the three and two pion decay modes of a single particle.
C.S. Wu quickly tested parity conservation in beta decays of Co60 and discovered that parity is 100% violated. Neutrinos are "left-handed", their spin is always anti-parallel with their momentum.
These results were immediately confirmed by other experiments. These, or similar experiments, could have been done 30 years earlier. (In fact, some experiments probably saw parity violating effects in the 1920's, but nobody realized it since nobody expected it. Part of the problem was that the idea and importance of "parity" was only recognized in the 1930's by Wigner.)
The q+/t+ is now known as the K+.
Charge conjugation reverses all "charges", e.g electric charge, baryon number, lepton number, strangeness, muon number, ….
Positions, energy, momenta, angular momenta, and spins are not affected by the C operator.
If y is an eigenstate of of charge conjugation, then
where the eigenvalues of the observable are PC=±1 because
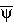 = PCC
= PCC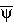 = PC2y
= PC2yA wavefunction may be in an eigenstate of C
if all additive quantum numbers are zero. Electromagnetic fields are produced by charges which change sign under charge conjugation, so
The C parity of neutral fermion-antifermion systems can be determined either by experiment, or by more detailed relativistic quantum analysis giving C=(-1)L+S.
(Where the particle symbol represents the "charge" part of the particle wavefunction.) Particles which are not their own antiparticles cannot be eigenstates of C, e.g.
If charge conjugation is a symmetry of the physics, then the charge conjugation eigenvalue is a multiplicative conserved quantity. Strong and electromagnetic interactions conserve C (e.g. p0Þggg is forbidden); weak interactions do not conserve C.
CP is the combined charge conjugation - parity operator. The weak interaction violates C and P a 100%, but CP is almost conserved. The only place this CP violation has yet been observed is in the the nutral kaon system.
Strangeness eigenstates:
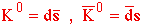
CP eigenstates:
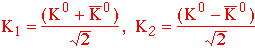
Mass eigenstates:
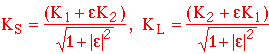
K2Þppp
is allowed, but K2Þpp
is forbidden by CP invariance. The KL ("K-long")
is mostly K2 and has a much longer lifetime than the
KS ("K-short") because there is so little
phase space for KÞppp
decays relative to K2Þpp
decays.