L = mr2 ![]()
" Science is facts; just as houses are made of stones, so is science made of facts; but a pile of stones is not a house and a collection of facts is not necessarily science."
-- Poincaré
We finished Chapter 9 by introducing the angular momentum, and then made a good start on Chapter 10 - Energy. I diverged from the textbook a few times in class today, and therefore will review that material a little more carefully than usual below.
Although the text doesn't do it until Chapter 13, I thought it would be worthwhile to discuss the fact that the linear momentum is:
p = mv
while the angular momentum can be writte as:
L = mr2
Both of these are some quantity involving the mass times a speed. This leads us to suspect, correctly as it turns out, that the quantity mr2 will appear in our equations for rotational motion in the same that that the mass appears in the corresponding equations for linear motion.
|
||
The above photographs are of Amin, a PHY138 student
from three years ago, serving a tennis ball. |
In order to maximise the speed of the serve, Amin needs to get the part of the racket that contacts the ball going at the highest possible speed. He does this with four lever arms:
Note that at contact, all four of these levers are at the maximum values as he "uncoils" into the serve. For each, the speed about the axis of rotation is given by:
r
where the angular speeds and radii are different numbers for each of the four rotations. Of course, except for the fourth rotation, the pivot point is also moving at the moment of impact.
Thus the speed of the racket as it contacts the ball is as large as possible. One of the suggested problems from Chapter 9 explores the tennis serve further.
I asked the text's Stop To Think 9.6. About 75% of the class got this question correct. Reminder: it is really worth your while to do all of the Stop To Think questions in the text and be sure you understand why the correct answer is correct.
In this section the text has a lovely introduction to the concept of energy as a "natural money." We didn't discuss this in class.
The origins of this treatment go back to at least Richard Feynman, who was a master teacher and also won a Nobel Prize in physics.
| I recently wrote a little document with much in common with both Knight and Feynman's approach. If you are interested, it is available via the link to the right. |
| We did a demonstration in class. A Flash animation of the the demonstration is available. We asked the class to predict that results of the demonstration before we did it. |
80% of the class answered C: they arrive at the same time. About 20% of the class answered A: the ball on the straight track arrives first.
The demonstration, as well as the Flash animation, show that in fact the right answer is B: the ball on the curved track "wins" the race. Only 13 students gave this answer.
| Some people find that thinking about the problem in terms of skiers instead of balls on a track is helpful. A Flash animation of this case is also available. |
In class I introduced the concept of a field. Since this is not in the textbook, here I will review that discussion.
In Newton's original description of gravitation, the Earth exerts a force w on a mass m as a long-range action-at-a-distance interaction. However, it is possible to break the description of this interaction into 2 parts: |
 |
It turns out that the simplest possible definition of Eg is best. If, as usual, we choose the y axis to point upwards, then near the surface of the Earth we say the gravitational field is:
Then the force exerted on a mass is just the mass times the field:
This approach to forces will be used heavily in the 3rd Quarter of PHY138.
But we can begin to see the value of a field description now. We have been talking about the gravitational potential energy, and have also been discussing how the overall energy of an isolated system is conserved. But exactly what is the gravitational potential energy? It turns out that it is just as real as the other forms of energy, and is stored in the gravitational field.
At the end I did a derivation very similar to one in Chapter 11, whose result I will use at the beginning of our next class. Here is an overview of that derivation. If you are taking MAT135 you will discover that in addition to an important Physics result, I am also introducing some facts about integration.
| We will be building on a Flash animation we used way back in Class 4. For your convenience, here is another link to that animation. |
First we consider a plot of force versus distance as shown. We construct
three rectangles of equal width You can probably already anticipate that I am going to end up increasing
the number of rectangles and taking the limit as |
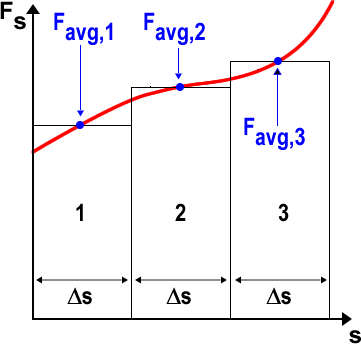 |
If ![]() s is
reasonably small, then the average acceleration of the object in region 1 is
as given by the kinematics for constant acceleration:
s is
reasonably small, then the average acceleration of the object in region 1 is
as given by the kinematics for constant acceleration:
| (1) |
We can similarly write a simple expression for the average speed in region 1:
| (2) |
From this we can write that the distance travelled is just the average speed tiimes the time:
| (3) |
Now we use Newton's 2nd Law and Eqn. 1 to get:
| (4) |
We use this and Eqn 3 to find the area of rectangle 1.
| (5) |
The times cancel out, so with some trivial algebra we get:
| (6) |
We can go through the same steps for region 2 to get:
| (7) |
When we add up the areas of regions 1 and 2, we get a cancellation because v2,i is equal v1,f so:
| (8) |
Adding the third region to the sum, increasing the number of
rectangles to infinity in the limit as ![]() s goes
to zero we end up having proven that:
s goes
to zero we end up having proven that:
The total area under a force versus distance plot is just the
change in kinetic energy. |
| Pdf version of the PowerPoint on the side screens. | |
| Today's Journal. |
| The arrows let you jump to the previous/next class summaries. |