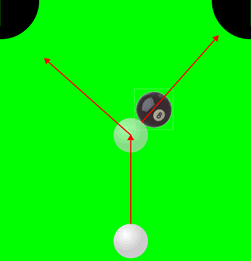
We discussed a two dimensional elastic collision between
2 objects of equal mass where initially one mass was moving and the other
was stationary. Then, in the absence of spin, I proved that after the
collision the angle between the 2 velocity vectors is ![]() /2
radians, or 90 degrees.
/2
radians, or 90 degrees.
Examples of such collisions are in playing billiards or in curling.
The figure illustrates for a game of pool in which the player is trying to sink the 8 ball into the right-hand pocket. If from the point of collision the angle between the path to the right-hand pocket and the path to the left-hand pocket is 90 degrees, then if the 8 ball goes into the right-hand pocket the cue ball will go into the left-hand one. This is a "scratch" and causes the player to lose the game.
Good players learn how to put spin on the cue ball to avoid the scratch. Beginning players should avoid trying to make such a shot.