PHY138Y - Mechanics - Class 8 - Wednesday October 5, 2005

Introduction

"I seem to have been like a boy playing on the seashore, and diverting myself now and then finding a smoother pebble or a prettier shell than ordinary, whilst the great ocean of truth lay all undiscovered before me."

-- Newton

Announcements

The PHY138 Mechanics home page neglected to list the last MP Problem Set of the quarter. This has been fixed. It will be on Chapter 13, and will be due on Friday, October 28 by 5 PM.
There is a Drop-In Centre in which you may ask any physics question. It is staffed by graduate student teaching assistants. It is located in MP200, which is on the 2nd floor immediately above the coffee stand in the lobby. It will begin operation on Tuesday October 11. It is staffed Mondays through Thursdays from 10 AM to 2 PM. The week before a test it will be open Mondays through Thursdays from 10 AM to 5 PM.

Pre-Class Quiz Chapts 7 - 8

This quiz was due last Monday, October 3.

I left out a minus sign in the third question about Newton's 3rd Law, and didn't get it fixed until late last week. All students get credit for this question.

For the remaining 3 questions, the mean was 86.7%

Today' Class

We finished our discussion of Chapter 7 by talking about §7.6 - Nonuniform Circular Motion. I introduced the angular acceleration which is given the symbol alpha ; the textbook does not do this until §13.1. I then wrote the kinematic equations 7.35 using the angular acceleration.

I stressed the similarity of these equations to the corresponding constant linear acceleration equations 2.18 and 2.22. PowerPoint slide number 7, available in pdf form below, shows that the form of these equations are identical.

We then analysed the situation discussed in Example 8.3. We analysed the two masses together as the system and solved for the acceleration. Next we analysed block B alone and found the force A exerts on B. We analysed block A alone and found the force B exerts on A. We noted that F_{A
on B} is equal and opposite F_{B
on A}.

We then analysed the situation shown in the figure. Again the surface is frictionless.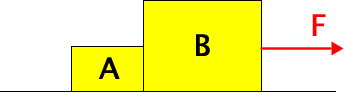

As before, we analysed the two blocks together and then separately. We again found that F_{A on B} is equal and opposite F_{B on A}.

Newton's 3rd Law says that the forces two objects exert on each other are always equal and opposite. This justifies something we've been doing all year: combining two or more objects together into the system under consideration and modeling the system as a particle. The internal forces various parts of the system exert on each other always cancel out.

Next we extended our analysis to the situation shown. We assumed that the string S is massless.

Because the string is massless, we showed that the tension S exerts on B, T, is equal and opposite to the tension S exerts on A, T'. Note that this is not Newton's 3rd Law.

Finally, we considered this system when the string has a mass m_S. In this case T and T' are not equal and opposite: their difference is m_Sa.

Because of Rosh Hashanah, some students could not attend this class. Thus this summary is more complete than has been or will be typical. You can follow the analysis in more detail in today's journal.

About Notation

Questions both in class today and after indicate that many of you are still a bit confused about notation, components, and vectors. Here I'll try to clear up some of the confusion.

Say I have two equal and opposite forces acting on some on some object, as shown.

In terms of the magnitudes of the forces I can write:

F_net = F₁ - F₂ = 0

Note that we are defining the positive direction to be to the right, as usual. Thus I am talking about the horizontal component of the two forces and there is a minus sign in the above.

If I write this in vector form it is:

Note that in this case there is no minus sign: the net force is the vector sum of the two forces.

In class today I did the examples first in terms of the components, the first form above, and often to try to clarify would then re-write it in vector form. I hope I got the notation right in all cases.

Say I am solving a complicated problem using the component notation. The Free Body Diagram indicates in which direction I think the forces are pointing. If I end up having made a wrong choice, then the force will come out to be negative. This means that it is actually pointing in the opposite direction to the way I drew it in the FBD.

In-Class Question

Here is a question we asked in class. The correct answer is 2: the two forces are equal and opposite but are not the action/reaction pairs that are the subject of Newton's 3rd Law. Almost all of you got the correct answer: well done!

Ballistocardiogram

We discussed the ballistocardiogram in class. Supplementary Notes on this topic have been prepared.

Check Your Understanding

Here is a small problem which you may wish to do in order to check whether you understand forces and tensions. It will not be collected, and is only for your amusement and edification.

The last example we did in class is of the blocks A and B connected by a string with mass m_S. Assume that the string is uniform and has a total length L.

What is the tension in the string at point right at its middle?
Devise an equation for the tension in the string at an arbitrary point along its length x. In assessing your answer, in addition to the usual criteria make sure it matches the answers we solved for in class at x = 0 and x = L.

Class Materials

Pdf version of the PowerPoint on the side screens.
Today's Journal.

I Screwed Up!

In class I screwed up the massive string case. The correct value of the force that the string S exerts on block B, F_{S on B} = T = (m_A + m_S) F / m_tot.

I have corrected the PowerPoint pdf linked to above. I have also corrected the Journal linked to above; the correction is in purple. Both of these changes were released on Tuesday, October 11.