This document discusses the metabolic rate of different animals, and how it scales with the mass of the creature. Much of the discussion is similar to one that appears in Jerry Faughn, Life Science Applications for Physics (Thomson, 1998), pg. 51 ff; this book is part of the package that accompanies the textbook for PHY138. Sadly, there are some problems with the data presented by Faughn, and his analysis does not go as far as we do here.
As realised by the physician Julius Robert Mayer in work he published in 1842, the metabolic processes of the body generate heat. This heat is radiated away from the body as thermal radiation.
The basal metabolic rate (bmr) is the rate at which the body generates heat energy when the organism is at rest. Note that the SI units of the bmr are watts. Other common units include kcal/day.
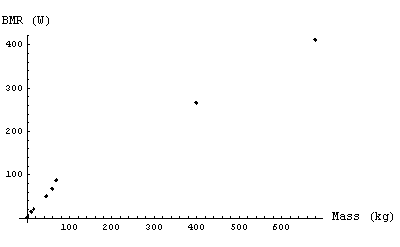
The table shows some typical values for the bmr of various animals as presented by Faughn.
| Animal | Mass (kg) | Basal Metabolic Rate (watts) |
|---|---|---|
Dove |
0.16 |
0.97 |
Rat |
0.26 |
1.45 |
Pigeon |
0.30 |
1.55 |
Hen |
2.0 |
4.8 |
Dog (female) |
11 |
14.5 |
Dog (male) |
16 |
20 |
Sheep |
45 |
50 |
Woman |
60 |
68 |
Man |
70 |
87 |
Cow |
400 |
266 |
Steer |
680 |
411 |
These numbers are "generic" in the sense that there are large variations among individuals.
Sadly, as is common for biological data taken or compiled by people who have not taken the PHY138 laboratory at U of T, there are no errors given with the above numbers.
| Clearly, there is some relationship between the mass and the bmr: more massive animals have higher basal metabolic rates. The plot to the right shows the data. |  |
Consider a resting woman whose metabolism is generating 68 watts, almost the same power as a 60 watt light bulb. If her body is radiating energy at a rate of 68 watts, then she is in equilibrium. If her body is not radiating this much power she will become warmer, and if she is radiating greater than 68 watts she become cooler.
Now, the rate at which heat energy is radiated from an object is proportional to the difference in temperature between the surface of the object and the temperature of the surroundings. This is usually called Newton's Law of Cooling.
In the 1840's Mayer noticed that people who lived in Indonesia had blood which was a deeper red than people living in Europe. This indicated that they had less oxygen in their blood, which meant they were consuming less energy. He reasoned that this was because to maintain equilibrium with their warmer environment required a lower metabolic rate. This was one of the very first realisations the heat is just another form of energy.
There is another factor that relates to the radiation of heat energy, the surface area A of the body doing the radiating. In terms of the power, i.e. energy per time:
(1) |
Here k is a constant. This relation explains
why, for example, air cooled motorcycle engines have fins: this greatly increases
the effective surface area so the engine radiates heat at a much faster rate.
Imagine we have 2 objects with the same shape but different sizes.We characterise the size of the object by some length L. For a sphere L might be the radius or diameter, for a cube it might be the length of one of the sides, for an elephant it might be the height. Regardless of the choice for how we characterise the size of the objects, the surface area scales as:
(2) |
For different species of animals, we might expect this scaling to also be approximately true, although the effective surface area of, for example, an animal with fur is greater than the effective surface area of an animal of the same size but with no fur.
For an object with density ![]() and volume V the mass m is:
and volume V the mass m is:
(3) |
For different objects characterised by some length L the volume scales as:
(4) |
Since, from Eqn (3), the mass is proportional to the volume, it is proportional to the length to the third power:
(5) |
We can state this same relation by saying that the length is proportional to the cube root of the mass:
(6) |
Then the square of L scales as the mass m to the two-thirds power:
(7) |
We saw in Eqn (2) that the surface area scales as the square of L, so in terms of the mass:
(9) |
In the previous section we saw that the rate at which an organism gives up heat to its surrounding is proportional to the area, Eqn (1), so we now see that it is proportional to the mass to the two-thirds power:
(10) |
where c is a constant.
But, we have seen that at equilibrium the rate at which the organism radiates energy is proportional to its metabolic rate. Therefore we predict that the basal metabolic rate of different organisms should scale as the two-thirds power of their mass.
(11) |
This type of dimensional analysis leading to Eqn (11) is often called allometry.
Experimentally, to investigate the validity of Eqn (11), it is convenient to take the logarithm of both sides:
(12) |
Then we can fit the logarithm of the basal metabolic rate versus the logarithm of the mass to a straight line. The intercept of the result of the fit is ln(c) and the slope should be two-thirds.
However, as first determined by Kleiber in 1932, the result of the fit gives a slope of 3/4. So experimentally Eqn (11) is not correct. Instead:
(13) |
Eqn (13) is called Kleiber's Law, and has been shown to be approximately true over 18 orders of magnitude in the value of the mass, from microbes to whales!
Other relationships involving living organisms show similar scaling as the three-quarter power of the mass. Examples include brain mass, lifetimes, etc. Other properties scale as the one-quarter power or similar values of the mass: examples include the heart rate (1/4), life span (-1/4), and the radius of mammalian aortas and tree trunks (3/8).
Various attempts to explain these facts have been made. One particularly interesting approach is by West, Brown and Enquist in 1997. West is a High Energy physicist, and Brown and Enquist are ecologists.
The figure to the right is a representation of the circulatory system. It shows how the arteries, in red, branch into smaller arteries, and finally into the capillaries; the capillaries then coalesce into small veins, in blue, which in turn coalesce into still larger veins. The original source of the figure is |
 |
West, Brown and Enquist realised that the above figure is very similar to a fractal, which you may know are objects with non-integer, i.e. fractional, dimensions. A very brief introduction to fractals is available here.
In their analysis, then, the metabolism scales as the dimension of the circulatory system, which is after all what delivers the energy being metabolised.
The details of their analysis is somewhat beyond the level of PHY138. Essentially, their main hypothesis is that to supply metabolising units (cells in organisms, respiratory molecules in mitochodria and cells), there are fractal-like, volume filling transport systems. They also assume:
This work has generated a huge amount of controversy. Giving the string "West Brown Enquist" to your favorite search engine will return a large number of documents.