PHY138Y - Mechanics - Class 3 - Monday Sept. 17, 2003

Introduction

More from John A. Wheeler on Problem Solving:

“One of the biggest problems is how to state the problem. It's an old saying that the minute you can state a problem correctly you understand 90 percent of the problem.”

Administration and Organisation

ROSI

Do not use ROSI to change your tutorial or laboratory section. See Dr. Savaria, MP901A, to change your tutorial section. See Dr. Serbanescu, MP124, to change your laboratory section.

Tutorials

Tutorials begin this week. You can find out where your tutorial group meets either:

• From the course bulletin board. This is located on the West wall of the North wing of McLennan.
• Via the web at STORM (STudent Online Record Management)

The URL for STORM is: http://www.storm.utoronto.ca/PHY138Y1Y/student/. Note that:

• The URL is case-sensitive. Do not use lower-case letters in place of upper-case ones and vice versa.
• The trailing slash / in the URL is required
• You will need to login to the site. The login is your student number, and the password is your last name exactly as it appears on your student card.
• If you get the URL and/or the login and/or the password wrong more than a few times, the system will not let you in no matter what URL and login and password you give. This is a desirable security feature. In this case, you must exit your browser and restart it.

Bookmarking this site once you are successfully logged in can save you having to re-type to URL in the future.

Problem Set #2

The problem set is due Monday, Sept. 22 at 5PM in the appropriate "Drop Box." The Drop Boxes are located in the basement of McLennan, under the main staircase. On the first floor, the staircase is located near the bust of Newton.

These problems are from the textbook:

• Chapter 1: Numbers 9, 58, and 65
• Chapter 2: Number 4

Supplementary Problem

This problem is not from the textbook.

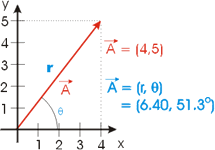
A vector has Cartesian coordinates of (4, 5), as shown.
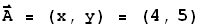
The same vector can be completely specified in terms of its polar coordinates r and where r is the magnitude of the vector and is the angle it makes with the x axis.

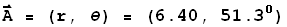
Of course, the relation between these two coordinate system's representation of the vector is:

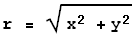
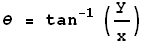
A second vector B has Cartesian coordinates (4, 2).

1. Express B in polar coordinates.
2. Find A + B by adding the Cartesian coordinates. Express the answer in polar coordinates.
3. Add the polar coordinates of A and B. Compare to answer 2.

Today's Class

We finished our discussion of the material in Chapter 1.

You should read §1.11 now. We deferred in-class discussion until we are doing some real analysis and problem-solving in class.

We then began Chapter 2. Our discussion extended the one in the textbook a bit; this will mean that we will have already covered some material in Chapter 3 by the time we are done. We discussed all but §2.7.

We used a Flash version of the textbook Figure 2.11. You may access it by clicking on button to the right. It will appear in a separate window and has a file size of 27k. Note that this is the first animation that we have shown this year that requires at least Version 6 of the Flash player; if the animation doesn't work for you then you should consider upgrading your version of the player.
For constant acceleration, as in textbook §2.6, we saw that from the graph of x as a function of time, we can use slopes (i.e. derivatives) to get v vs. t, and then a vs. t. We then saw that we can go the other way: from a vs. t we can compute the area under the curve (i.e. the integral) to find v vs. t, and from that the area we get x vs t. The Flash animation we used may be accessed by clicking on the button to the right. Separate window; Flash 6 or better; 30k.
You may access the "Journal" file I wrote in class with the button to the right. Separate window; 150k.

The arrows jump to the previous/next class summary.