Firstly we notice that electrons are truly point particles; those that
get through the double slit system and reach the detection screen arrive
at one place and one place only on that screen.
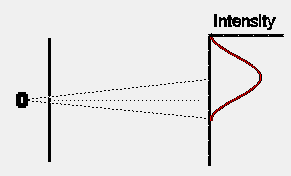
If we were to close one slit and wait for some time to allow a large
number of electrons to reach the detection screen, the distribution of
electrons would look somewhat as shown opposite. The intensity pattern
is spread out somewhat, presumably because some of the electrons are scattered
off the edges of the slit. Note that, as expected, the centre of the intensity
pattern lies at a point in the direct line-of- sight back to the electron
oven, and is displaced slightly from the exact centre of the detection
screen.
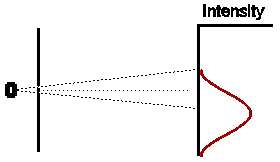
In a similar way, if we were to close off the other hole, and open the first for the same amount of time, we would expect (given that our experiment has been set up with exact symmetry) that the intensity pattern would be identical in shape to the first case, but displaced an equal amount to the other side of the centre of the detection screen.
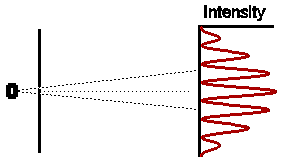
So if both slits were left open for the same amount of time, what would
we expect ? Obviously, if electrons were classical particles, we would
expect that the total intensity pattern is simply the sum of the two previous
intensity patterns, shown opposite.
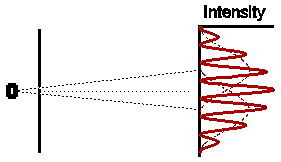
Astonishingly, this is not at all what we observe. In fact the
observed intensity pattern shows interference bands, very similar to those
produced by light passing through the double slit system; there are places
on the detection screen where no electrons land, and other places where
more electrons than the number we would expect from simply adding the contributions
from each slit acting alone.
NOTE: Dr David Harrison teaches the second half of the course JPU200Y that covers some of the material also covered in PHY100F. He has constructed a beautiful description of the Double Slit experiment on the web pages of that course. I do urge you to look at these pages - just click on http://faraday.physics.utoronto.ca/GeneralInterest/Harrison/DoubleSlit/DoubleSlit.html
Click here to return to top of document
We might be concerned that some sort of interference effect may be going on between different electrons as they traverse the experimental system. To check this, we could reduce the intensity of the electron beam (by turning down the oven, for example) so that at any one time there was only one electron in the system. The extraordinary result is that, although it takes much longer for the interference pattern to develop, exactly the same pattern does develop.
But how can each individual electron "know" where it is supposed to land up, since the experiments tell us that this depends only on whether one or both slits are open. So maybe the electron somehow splits itself up and goes through both holes at once, recombining before it reaches the detection screen. To check this, we could design an apparatus to check whether the electron goes through one slit or the other, or both, when both slits are open .
Let us suppose that we have a small light placed just behind the double slit system. It sends out photons to bounce off the electrons that are coming through the slits; if an electron is hit, it deflects the photons into our eyes, and we observe the electron and can determine its position. (Of course this is a very crude piece of equipment to make such a measurement; in reality we would design things much better. However this "gedanken" experiment makes the discussion simpler, and represents the essentials of a real experiment). Now we can see which slit each electron comes through. What is the result? It turns out that indeed, every time theelectron comes through one slit or the other. However we notice to our dismay that when we are making this observation, the interference pattern disappears!
Perhaps we have so many photons around that they are somehow interfering with the electrons' paths? Well, we can reduce the intensity of the light source (i.e. the number of photons flooding the system) to check this out. However, if we reduce the intensity too much, we will begin to miss some of the electrons, because there aren't enough around to ensure that every photon is struck, and thus observed. If we look at the distribution of the electrons that we miss, indeed the interference pattern is again observed. However, for those electrons for which we can determine which slit they have passed through (and, when detected, they are always seen to come through one slit or the other!), no interference pattern is observed.
Perhaps, we might suggest, the photons we are using in this experiment are too energetic, so that their impact on the fragile electrons is too large. Well, we can reduce their impact by reducing their momentum; since their wavelength is inversely proportional to the momentum, that means we increase their wavelength. And indeed as we increase the wavelength of the observing photons, we do begin to
notice that the interference pattern re-establishes itself. However, to our dismay, just at that point we find that our resolution (which, remember, is proportional to the wavelength of the observing light) has become so poor that our ability to determine which slit these electrons have come through disappears!
In the words of Richard Feynman (in The Character of Physical Law. (MIT Press)):
"If you have an apparatus which is capable of telling which hole the electron goes through ... then you can say that it either goes through one hole or the other. It does; it is always going through one hole or the other - when you look. But when you have no apparatus to determine through which hole the thing goes, then you cannot say it goes through one hole or the other ... to conclude that it goes through one hole or the other when you are not looking is to produce an error in prediction. That is the logical tightrope on which we have to walk if we wish to interpret Nature."
Now it may be thought that our inability to pin the electron down to one slit or the other at the same time as we are observing the interference pattern is simply due to the fact that our observation of the system disturbs it too much. There is indeed some truth to this; most modern scientists would now accept that the old idea that the observer can stand outside of Nature in order to observe it is no longer tenable. John Wheeler has put this nicely, by saying that indeed there is no such thing as an "observer" - only "participants". However, there is something even deeper going on here: for if we had any method whatsoever to determine which slit each electron came through, simple logic would insist that the observed distribution would simply be the sum of the distributions of electrons from each slit, taken separately. That is, we should observe
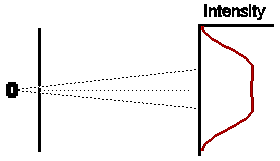
Nature would then be placed in an irresolvable paradox. So the implication here is that indeed the future is unpredictable; we can never predict which slit the electron is going to go through.
Click here to return to top of document
Heisenberg's Uncertainty Principle.
There is a more formal mathematical statement of this fact, called the Heisenberg Uncertainty Principle, which sets clear limits on what we can observe. A simple "sort of proof" goes as follows:
Consider our attempt to view the electrons in the double slit system
by shining light of wavelength 
on them. The photons of this light will have momenta pphoton
= h/.
If we manage to see an electron it will be because one of these photons
has struck it. Clearly the electron momentum will have been affected by
this interaction with the photon. Let us call the change we have so induced
in the electron's momentum
pelectron
(meaning a small change in pelectron). Obviously,
the greater the momentum of the photon, the greater this change in the
momentum of the struck electron. Certainlypelectron
is proportional to pphoton; the constant of
proportionality will depend to some extent on the experimental set-up,
but might typically be of the order of 0.1 or so. However, to the order
of our present calculation, we can assume it is 1. Thus we can write that pelectron
= pphoton
= h/ .
Now we know that the precision with which we can determine a distance
is limited by the size of the wavelength of the light which we use to measure
the distance. In fact this uncertainty in position is directly proportional
to the wavelength of the light; again, at our present level of accuracy,
we can set the proportionality constant to 1. In the double slit experiment,
let us call this uncertainty in position x.
So, using the above arguments, we can write the uncertainty in our knowledge
of the position of the electron, determined by shining a photon of wavelength
L on it, to be xelectron
= . Combining
the two equations for the uncertainty of the electron's momentum and its
position, we obtain the following expression for their product:pelectron. xelectron
= (h/)
= h. It turns out that this expression is generally true for all particles,
and we can write it finally as p
. x = h.
This is one way of writing Heisenberg's Uncertainty Principle.
The difficulty with this derivation of the Uncertainty Principle is that it may encourage you to think that the uncertainty in the result, and indeed an explanation of the whole odd behaviour that we observe in the Double Slit experiment is entirely due to the unavoidable disturbance that we make when we observe the experiment.
However this is simply not true. The Uncertainty Principle implies a built-in, unavoidable limit to the accuracy with which we can make measurements. NOR is it similar to experimental uncertainty as understood in Classical Physics. There, for example, when we want to measure the temperature of a beaker of water, it is certainly true that we disturb the temperature we want to measure by introducing a cold thermometer into it, so the temperature we measure is thus not exactly that of the beaker alone. However, in principle, we can remove this error, by measuring with smaller and smaller ther mometers and extrapolating to zero size; in principle (if not in practice) we can thus measure to arbitrarily high accuracy. This is not possible in the Quantum world, thanks to Heisenberg's Uncertainty Principle. A further implication is that the future is not predictable in the classical sense; for if we do not know the initial conditions exactly - and Heisenberg's principle tells us that we cannot - we cannot make accurate predictions about the future, no matter how precise and pre-determined are our equations.