There are many many issues in designing a good test, and a huge literature on this topic. In this section we only discuss one consideration: how "difficult" should a test be?
We imagine an average class, although I don't think I have ever seen such a group of students. According to the University of Toronto marking standards, we want the mark distribution on a test to be:
| Mark on Test | Percent of Class |
|---|---|
| 0-49% (E, F) | 5% |
| 50-59% (D) | 10% |
| 60-69% (C) | 35% |
| 70-79% (B) | 35% |
| 80-100% (A) | 15% |
In order to keep the discussion simple, we imagine a test with exactly 10 questions, and also imagine that the test is graded with no part marks awarded. We also imagine that the people who set the test managed to achieve the U of T grade distribution shown in the above table.
95 percent of the class got five or more of the questions on the test correct; only five percent of the class failed the test. Further, for the students who did pass the test, each question on the test was worth one entire letter grade.
I will argue that this test is not well-designed.
First, we have asked five questions out of ten that every student except a small group of 5% have answered correctly. This seems to be a waste of most students' time and a waste of the the available "test space."
Also, for the vast majority of students who passed the test, any mistake on a single question costs them an entire letter grade. This seems pretty harsh.
I claim that a good test tries to emphasise differences between students. I also claim that a good test doesn't waste half of its "space" trying to tell whether or not a particular student has passed. In fact, as an instrument for differentiating between students the ideal test should have a distribution something like:
| Letter Grade | Raw Test Mark |
|---|---|
| E,F | 0 - 19% |
| D | 20-29% |
| C | 30-49% |
| B | 50-79% |
| A | 80-100% |
For our "normal" class, this test ends up with a class average of about 53% and a median of 50%.
Notice that in this test we have only asked two questions that are so easy that if a student misses one or both plus all the rest of the questions they fail; the rest of the questions distinguish between D, C, B and A grades. For each letter grade there are two or three questions, so a single careless mistake on a question is not as devastating for the final grade.
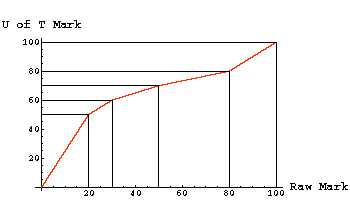
Of course, this raw mark must be converted to U of T numbers. The following graph shows the mapping:

It is the U of T Mark that is recorded and used in determining the student's mark in the course.
The major problem with using such a well-designed test is that at first it is a bit of a shock for students. An average student is used to getting 70% or so of the questions on a test correct, and if they are only getting about half the questions correct fear that they are failing. My experience, however, is that once such a student gets used to the fact that the test is "harder" than they are used to, the anxiety quickly dissipates. It is, of course, vital that one spends a lot of class time before the first test explaining to the class how the test is being designed. Also, when setting the test if in doubt on asking a particular question choose the easier alternative; having the average a bit too high is better than a bit too low.
As indicated at the beginning, we have only discussed one aspect of test design. Here I shall briefly mention a few other opinions and observations about tests. I ignore a troubling truism: part of what we are testing is the ability of a student to take tests.
First, often we are not asking what we think we are asking
For example, I have data that show that "trivial" changes in the wording of a question can have dramatic effects on student performance. The wording changes were guided by a Piagetian analysis, but I don't think that theoretical framework is the key. In any case, the changes were only trivial to the person setting the test.
Second, once when I was teaching a large first year course we set multiple choice tests that were graded by computer. The computer allowed us to compare how students did on a particular question to how they performed on the test as a whole. Questions with a low correlation are clearly poor. It was shocking to see how many poor questions we were asking. Usually once we had used the analysis to identify a poor question we could re-read it and see why. Once again, these poor questions were not asking what we thought they were asking.
In this same large course, the Final Exam was a three-hour format with about thirty questions. Grading by computer allowed us to analyse the reliability of the test instrument. Although we put a huge effort into setting a good test, the statistics indicated that if we gave the same students a similar test their final marks would match their marks on the Final Exam only to within about one-third of a letter grade. This means that the best exam we could design was only accurate to about three or four percent in the final grade. Sometimes we didn't do even that well, and in a one-hour test with fewer questions our tests were only accurate to about six percent. Making the test "hard" as defined in the previous section increases the accuracy of the test.
Finally, I close with a famous but probably apocryphal story. A Physics student was writing a test on which the following question appeared:
The student answered: "I would take the barometer up to the roof and drop it onto the sidewalk below. By measuring the time it takes to fall I can calculate the distance according to 1/2 g t2."
The professor marked the question wrong, and the student appealed to the Department Chair.
In the subsequent interview the Chair asked the student if he knew any other answer to the question. The student replied that he did. "I will take the barometer down to the basement of the building and find the superintendant. I will say to him 'Sir! I have this fine barometer that I will give you if you tell me how tall the building is.'"
The professor had originally been seeking an answer involving using the barometer to measure the difference in atmospheric pressure between the ground and the top of the building. Such an experimental technique turns out to be pretty inaccurate. In fact, the student's original answer would have been much more accurate than the answer the professor had been looking for.
This document is Copyright © 1999 David M. Harrison.