We can classify waves into 2 types:
A moment's reflection will convince you that a transverse wave can have the plane of the oscillation at different orientations. The plane is called the polarisation of the wave. The following figures illustrate for the electric and magnetic fields of a light wave; the electric field is represented by the red arrows and the magnetic field by the blue arrows. The two polarisations are at right angles to each other.
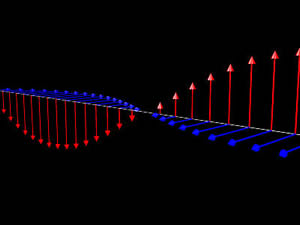 |
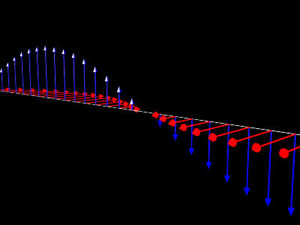 |
Light generated by, say, a light bulb is a mixture of all the possible polarisations; we call such a light wave unpolarised.
Polaroid filters are capable of selecting a particular polarisation state from an incident light wave. By convention the polarisation of a light wave is specified by the orientation of the electric field.
To the right we imagine an light wave incident from the left onto a polaroid filter. If the incident wave is unpolarised, then one-half of the wave will emerge from the polaroid filter. We call this orientation of the polaroid zero degrees, and the orientation is indicated by a red arrow. |
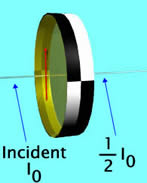 |
| If the incident wave is unpolarised, then the orientation of the polaroid filter doesn't matter: for any orientation of a perfect filter exactly one-half of the incident wave will emerge. The figures illustrates for an orientation of 45 degrees. | 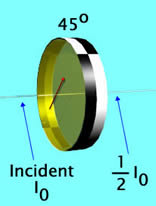 |
| If we place a second filter behind the first with the same orientation, the second filter has no effect: one-half of the incident beam emerges from the first filter and all of that beam emerges from the second filter. | 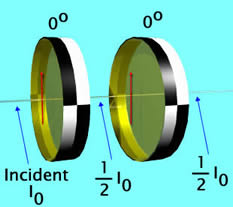 |
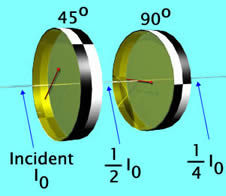
If the first filter is oriented at 0 degrees and the second filter is oriented at 45 degrees, one-half of the light incident on the second polaroid emerges. Thus one-half of one-half = one-quarter of the incident ray emerges from the combination of filters. |
 |
Similarly, if the first filter is oriented at 45 degrees and the second at 90 degrees, one-quarter of the incident beam emerges from the combination. In general, if the angles between the 2 filters is
This is called Malus' Law. |
 |
| If we place a second filter behind the first one that is oriented at 90 degrees relative to the first one, no light emerges from the second filter. This is perhaps expected, since the 2 polarisations that are being selected by the filters are perpendicular to each other. This is also the result predicted by Malus' Law. | 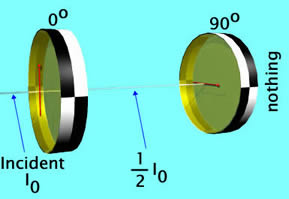 |
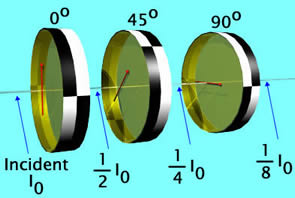
We have just seen that if the 2 filters are oriented at 90 degrees relative to each other, the second filter stops all of the light incident on it. Perhaps surprisingly, if we place a filter oriented at 45 degrees between these 2 polaroids, it turns out that some of the light emerges from the 90 degree polaroid. This can be viewed as a consequence of Heisenberg's Uncertainty Principle from Quantum Mechanics. |
 |
Edwin Land, a Harvard dropout, invented the polaroid filters discussed in the previous section, in 1926. Before then the main way of producing a polarised beam of light was using a property of reflected light which is discussed in this section.
In the figure to the right, 2 beams of light are incident from behind and above onto a slab of glass. The polarisation of the beam closest to you, as given by the orientation of the shown electric field, is parallel to the surface of the glass. The polarisation of the other beam is perpendicular to this. If the angle of incidence of the beams is at a critical angle, called the Brewster angle, then all of the beam closest to you is reflected and all of the other beam is refracted into the glass. This is the situation that is shown. If n is the index of refraction of the glass, then the Brewster angle is given by:
|
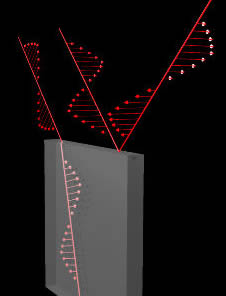 |
At angles of incidence not equal to the Brewster angle, the reflected ray will still have more of the polarisation parallel to the surface of the glass than the perpendicular polarisation. Good sunglasses include polarisers in their lenses to filter out this polarisation. Thus the lenses tend to filter out reflected glare.
This document was written by David M. Harrison, Dept. of Physics, Univ. of Toronto, harrison@physics.utoronto.ca in February 2005. This is $Revision: 1.4 $, $Date: 2005/02/26 10:57:23 $ (y/m/d UTC).
The text and images are Copyright © 2005 David M. Harrison.
 |
This work is licensed under a Creative Commons License. |