A Mathematical Supplement: Deriving Time Dilation
For Lou, we assume that the light source, light detector, and clock are
all located in exactly the same position, which is not exactly the way the
figure shows it. We will call the distance from the source to the mirror
d.
The two events whose times of occurence Lou will measure are:
- The light is emitted from the source
- The light is detected by the detector
Since the light travels a total distance of 2d and travels at a
speed c:
tLou = 2d / c
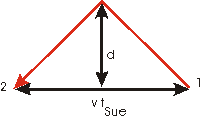 Sue observes the same two events, but
relative to her the light source, mirror and detector are moving at some speed
v to the left. We assume, correctly as it turns out, that the light
travels a vertical distance d relative to Sue also. The
horizontal distance between the two events relative to Sue is v
tSue, as shown.
Sue observes the same two events, but
relative to her the light source, mirror and detector are moving at some speed
v to the left. We assume, correctly as it turns out, that the light
travels a vertical distance d relative to Sue also. The
horizontal distance between the two events relative to Sue is v
tSue, as shown.
The total distance travelled by the light is:
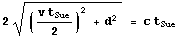
Note that the right hand side of the above equation uses the fact that
the speed of light relative to Sue is also c. The equation can be
rearranged to:
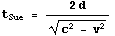
which leads to the time dilation relation that we are deriving.
If it were not for Einstein's explanation of the Michelson-Morley
experiment then if the speed of light relative to Lou were c, then the
speed of that same light realtive to Sue would be:
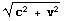
and the time between the two events as measured by Sue's clocks would be
the same 2 d / c as measured by Lou's clocks.
 Sue observes the same two events, but
relative to her the light source, mirror and detector are moving at some speed
v to the left. We assume, correctly as it turns out, that the light
travels a vertical distance d relative to Sue also. The
horizontal distance between the two events relative to Sue is v
tSue, as shown.
Sue observes the same two events, but
relative to her the light source, mirror and detector are moving at some speed
v to the left. We assume, correctly as it turns out, that the light
travels a vertical distance d relative to Sue also. The
horizontal distance between the two events relative to Sue is v
tSue, as shown.