Click here to return to the Special Relativity document.
We consider the swimmers when the raft is being towed. We will imagine that the swimmers swim at a speed c relative to the water, and that the raft is being towed at a speed v relative to the water. We will also call the distance from the raft to the markers d.
For swimmer 1, he first swims to the right at speed c as the marker is moving to the left at speed v, both speeds relative to the water. We shall call the time from when he leaves the raft until he reaches the marker t1a. So:
d = t1a c + t1a v
or:
t1a = d / (c + v)
Swimmer 1 then turns around and chases after the raft. Call the time from when he leaves the marker until he catches the raft t1b. Then:
t1b c = d + t1b v
or:
t1b = d / (c - v)
The total time for swimmer 1 to swim the race is:
t1 = t1a + t1b = d / (c + v) + d / (c - v) = 2dc / (c2 - v2)
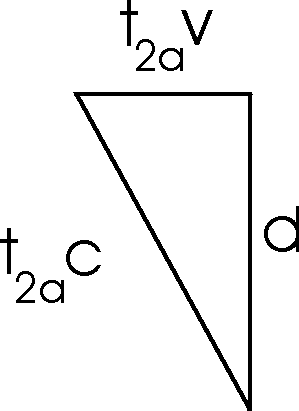
| Swimmer 2 swims out to the marker as it is moving to the left at speed v relative to the water. So he swims along the hypotenuse of a right triangle. We call the time for him to reach the marker t2a. |  |
A trivial amount of algebra yields:
![]()
It takes swimmer 2 the same time to swim back to the raft so:
![]()
Finally we compare the times for the two swimmers and get:
![]()
If you continue to follow the mathematical threads that appear here from time to time, the square root factor above will appear over and over in the theories of relativity.