Click here to go to the
UPSCALE home page.
Click
here to
go to the Physics Virtual Bookshelf
Click
here to go to the
JPU200Y home page.
![]()
This document was written in February 1999 by David M. Harrison, Department of Physics, University of Toronto, mailto:harrison@physics.utoronto.ca. This is version 1.7, date (m/d/y) 09/17/02.
This document is Copyright © 1999 - 2002 David M. Harrison.
This material may be distributed only subject to the terms and conditions set forth in the Open Content License, v1.0 or later (the latest version is presently available at http://opencontent.org/opl.shtml).
![]()
"A theory is the more impressive the greater the simplicity of its premises, the more varied the kinds of things that it relates and the more extended the area of its applicability. Therefore classical thermodynamics has made a deep impression on me. It is the only physical theory of universal content which I am convinced, within the areas of the applicability of its basic concepts, will never be overthrown." -- Einstein (1949)
![]()
We shall define the entropy in three different yet equivalent ways.
First we consider the probabilities for dice that every good backgammon players knows. Below, the left column indicates the sum of the two die; the next column lists all the possible combinations that give that sum; the third column counts the number of combinations for that sum. As you can see, there are a total of 36 different combinations for the two die, and each are equally probable to occur for "honest" dice. Thus the probability of getting a particular sum, as shown in the last column, is just the number of combinations divided by 36.
| Sum | Combinations | Number | Probability |
|---|---|---|---|
| 2 | 1-1 | 1 | 1/36=3% |
| 3 | 1-2, 2-1 | 2 | 2/36=6% |
| 4 | 1-3, 3-1, 2-2 | 3 | 3/36=8% |
| 5 | 2-3, 3-2, 1-4, 4-1 | 4 | 4/36=11% |
| 6 | 2-4, 4-2, 1-5, 5-1, 3-3 | 5 | 5/36=14% |
| 7 | 3-4, 4-3, 2-5, 5-2, 1-6, 6-1 | 6 | 6/36=17% |
| 8 | 3-5, 5-3, 2-6, 6-2, 4-4 | 5 | 5/36=14% |
| 9 | 3-6, 6-3, 4-5, 5-4 | 4 | 4/36=11% |
| 10 | 4-6, 6-4, 5-5 | 3 | 3/36=8% |
| 11 | 5-6, 6-5 | 2 | 2/36=6% |
| 12 | 6-6 | 1 | 1/36=3% |
The most probable result, occurring one-sixth of the time, is to get seven.
Surprisingly, the first known successful calculation of the above probabilities didn't occur until the sixteenth century, by Girolamo Cardano. An exploration of why this should have occurred so late, plus a great deal more about probability, is the wonderful book by Peter L. Bernstein, Against the Gods: the remarkable story of risk (Wiley, 1996), ISBN 0 471 29563 9.
The probabilities for dice lead us to our first definition of the entropy:
The entropy is a measure of the probability of a particular result.
Here, then, a seven is the result with the highest entropy (i.e. probability), and a 2 ("snake eyes") or a 12 ("boxcars") have the lowest entropy.
Technical note: The entropy is actually k ln(# combinations), where k is called Boltzmann's constant and ln means the natural logarithm.
| Now we consider a "box" with two white marbles and two black marbles inside it. The box is made so that exactly two of the marbles are always on the left hand side and two are always on the right hand side of the box. In the case shown to the right, both white marbles are on the left side of the box and both black marbles are on the right side of the box. There is only one combinations of marbles that gives this arrangement. | 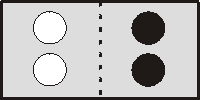 |
| Imagine that we shake the box, and how the marbles distribute themselves is random. Now we have a white marble and a black marble on the left, and a white and black marble on the right. Call the black marbles B1 and B2, and the white ones W1 and W2. Then for this arrangement we could have B1,W1 on the left and B2,W2 on the right. We could also have B1,W2 on the left and B2,W1 on the right; or B2W1 on the left and B1,W2 on the right; or B2,W2 on the left and B1,W1 on the right. Thus there are four combinations that give this arrangement of the marbles. | 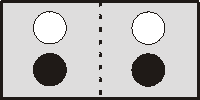 |
| Finally, we show the single arrangement with both black marbles on the left and both white ones on the right. |  |
| For the four marbles in a box that we just considered, there are a total of six equally likely combinations. The one with the highest probability (4/6=67%) has a black marble and a white marble on each side of the box. This is therefore the state with the highest entropy. The graph to the right shows the total number of combinations. |  |
| For six marbles, three black and three white, the equivalent plot is shown to the right. | 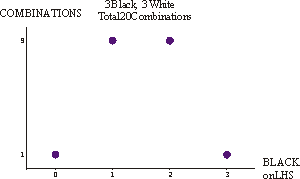 |
| Now we jump to a total of 12 marbles, six black and six white. (Here I did not find the number of combinations by brute force counting: I used some mathematics.) | 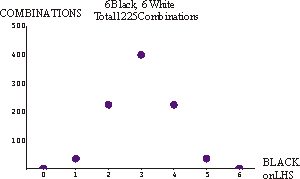 |
| Here is the equivalent plot for a total of 100 marbles. The thing to notice is that the most probable result remains 50% black on the left, 50% black on the right, 50% white on the left and 50% white on the right. However, as the total number of marbles increases, the "peak" becomes more sharp. This means that the probability of getting a result far away from 50% gets smaller and smaller the greater the number of marbles. You may wish to know that the total number of combinations for this case is about 1 followed by 29 zeroes before the decimal point. |  |
| For a total of 400 marbles, the point we just made about the peak becoming narrower becomes even more obvious. Here the total number of combinations is about 1 followed by 119 zeros before the decimal point. |  |
The conclusion from all this is that the most probable highest entropy result is the one in which equal numbers of white and black marbles occur on both sides of the box, and that as the total number of marbles increases the probability of getting a distribution very far from this most probable result goes down.
Imagine the case above with a total of 200 black marbles and 200 white marbles. If all the white marbles are on the left hand side of the box and all the black ones are on the right hand side of the box, we say that the marbles are very ordered. The state where all the all black marbles on the left and all the white ones are on the right are similarly ordered.
If we have 100 black marbles on the left, 100 on the right, 100 white marbles on the left and 100 on the right, we say the system is very disordered, which is another way of saying that the two sides of the box are undifferentiated. Note that this is also the most probable state.
Thus we are led to our second equivalent definition of entropy:
The entropy is a measure of the disorder of a system.
Caution: it is easy to get confused because this definition is the measure of the lack of order in a system. Usually we think of quantities such as mass, energy, etc. as measuring the amount of that something; here we are measuring the lack of that something. Some people like to talk about the negentropy, which is the negative of the entropy; it measures the order of the system.
You may know that people used to think that heat was some sort of fluid that could flow from one body to the other. This fluid was called caloric, and attempts were actually made to measure its mass by weighing a hot object and then re-weighing it after it cooled down.
Later Count Rumford and others eventually realised that heat was just another form of energy. In modern terminology we say that it is the internal energy of motion and vibration of the molecules of a substance.
This realisation that heat was energy was pretty exciting to scientists of the day. There is a perhaps apocryphal story that Joule got married and went on his honeymoon to a resort with a waterfall. He was so excited by the realisation that he spent all of his time measuring the difference in temperature of the water between the top and bottom of the waterfall; this caused his wife to leave him.
Since E=m c 2, there really is a change of mass of an object due to its heat although not due to the existence of caloric. This change of mass, however, is essentially unmeasurable. For example, if a 20 kg block of lead cools from 100 °C to 0 °C, the change of mass is about 3 trillionths of a kilogram.
|
For completeness, we shall also want to know about the absolute temperature scale. It is an experimental fact that if we take a quantity of gas at constant volume and measure its pressure as a function of its temperature in, say, Celsius, the relation will be a straight line. We can extrapolate that line back to the left to find the temperature when the pressure of the gas goes to zero. The result of the extrapolation is a temperature of -273.16 degrees. |
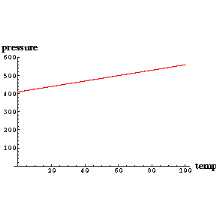 |
All gases exhibit this straight line relation between pressure and temperature. Further, if we do the extrapolation back to zero pressure, the result is -273.16 degrees for all gases.
The phenomenon of pressure is due to the molecules of the gas bouncing off the walls of the container. Thus, when the pressure has become zero we have stopped the molecules from moving around; this is another way of saying we have extracted all the heat from the object. Thus a temperature of -273.16 degrees is called absolute zero; it is the minimum temperature an object can have.
Thus nature seems to provide a temperature scale, which we call the Kelvin scale:
T(absolute, Kelvin)=t(°C) + 273.16
Now, imagine we have a system with 2 kinds of molecules:
When the molecules collide a high energy molecule can transfer its energy to a low energy one. So the energy can distribute itself in various ways. The molecule-molecule collisions are essentially random, so the way the energy gets distributed is also random.
Now, imagine we have a total of four molecules in the system, two of them hot and two of them cold. Represent the hot molecules as white spheres and the cold ones as black spheres. Then the ways the molecules can distribute themselves is exactly the same as the ways the four marbles, two black and two white, could distribute themselves in the first section above.
In fact, all those somewhat dreary arguments about marbles can now be carried over to arguments about the distribution of heat in a body.
We are now ready to state the third equivalent definition of the entropy:
The entropy measures the heat divided by the absolute temperature of a body.
We shall be a bit mathematical (actually "arithmetical") to see how this definition works.
Imagine the left side of the body is at 273 Kelvin, and the right hand side is at 373 Kelvin. We shall consider a small quantity of heat, say 0.001 Joules, being transferred either from the left to the right or the right to the left. We assume the amount of heat is so small that the two sides of the body do not change their temperature.
Thus, if the heat goes from the hotter right hand side to the colder left hand side, the total system is moving to a state of higher entropy. This is also the state with the higher disorder, since the differentiation between the cold and hot sides is diminishing. It is also the state with the highest probability, since more combinations of hot and cold molecules make it up.
![]()
In the previous section we developed three equivalent definitions of entropy:
Regardless of which definition we use, the Second Law of Thermodynamics states:
The entropy of a closed system "never" decreases.
We shall see soon why I have put the word "never" in quotation marks.
A common statement of the law is: "The heat never flows from the colder to the hotter." We have just seen in the previous section how the "official" form of the Second Law plus definition three for the entropy is consistent with this common statement.
Consider your refrigerator. It takes heat from the cold interior and deposits it in the warmer air of your kitchen via the coils on the back of the fridge. Does this violate the Second Law? No, because of the phrase closed system in the law. Even if the door is closed your fridge is not a closed system; it is connected to an outside power source via the cord plugged into the electrical outlet. Unplug your fridge and the heat will start moving from your kitchen into the fridge, spoiling the food.
We have just considered the third definition of entropy. Continuing to explore the list in reverse order, one implication of the second definition is that the Second Law says that, as Kurt Vonnegut says, the universe is turning into kibble. Another way of saying this is that if the universe is open then eventually it will be one with no differentiation: all parts will be of equal temperature. We will explore the consequences if the universe is closed soon.
Finally, the first definition of entropy reads that the less probable result never happens. This is not quite correct. Imagine the air molecules in a room: there is a non-zero probability that all the molecules will rush into the far corner of the room and we will all suffocate. But, as we have seen, if the number of molecules in the room is sufficiently large the probability is very very small. The number of molecules in a typical room is about 1 followed by 80 zeroes before the decimal point. So, the probability is so small that we, erroneously, say it can never happen. This is why I put the word "never" in quotation marks in the "official" statement of the Second Law of Thermodynamics; to be completely correct we should have said "usually."
![]()
The Second Law of Thermodynamics provides a definition of time's arrow. The law states that the entropy (usually) increases. And the increase occurs in time.
Imagine that we make a videotape of a "break" in a game of pool. We see 15 colored balls in a triangular configuration and a white ball coming in and breaking them up; the balls scatter in all directions.
If we run the videotape backwards we know immediately that this is (probably) not the correct direction for time.
If we reduce the number of billiard balls to, say, two, then a videotape of one ball colliding with another is just a possible as the tape running backwards. Here we see another manifestation of the fact that the determination of the direction of time from thermodynamics depends on having lots of objects in the system.
Another example is the relation between the scale of a physical system and the "correct" direction of time is milk swirling in water. A RealMedia video of this is available here. File size is 530k.
Thus the Second Law provides a definition of the direction of time. We know of two other definitions:
Later we shall explore whether there is any connection between these two clues to the direction of time and the Second Law of Thermodynamics.
![]()
"I think of my lifetime in physics as divided into three periods. In the first period … I was in the grip of the idea that Everything is Particles … I call my second period Everything is Fields … Now I am in the grip of a new vision, that Everything is Information." -- J.A. Wheeler
Above we defined the negentropy, which is the negative of the entropy. Thus the negentropy measures the amount of order in a system, which is just a reflection of the fact that the entropy measures the disorder.
The Search for ExtraTerrestrial Intelligence (SETI) project is scanning the heavens and monitoring radio waves etc. coming from deep space. Imagine that we receive a radio wave consisting bursts of signal interspersed with silence. We shall designate the signal as 1 and the silence as 0. One such burst might look like:
1000000010011100111010
The SETI people would take such a sequence and try to find patterns in it. In this case, they would be unlikely to find any since the digits were generated randomly by a small computer program. Similarly one could generate such a sequence by flipping a coin 22 times and assigning heads to be 1 and tails to be 0.
Here is another sequence to consider:
1011011101111011101101
This one has at least one pattern. The number of 1's separated by 0's are 1,2,3,4,3,2,1.
Thus the SETI project would pay a great deal of attention to the second sequence. Some years ago bursts of electromagnetic radiation were detected on Earth with a nearly perfectly constant time between bursts. The source of these signals, the pulsars, were investigated very carefully in case they were being sent by an intelligent being. Later is was concluded that the pulsars were actually rotating neutron stars left over from supernovae explosions of stars.
In the terms we have been using in this document, the second sequence of 1's and 0's is more ordered than the first, it has a higher negentropy.
This is true of any signal that is capable of carrying information. Thus, as Shannon realised 1948, information theory has a very close connection to thermodynamics.
To learn more about information and its growing role in the sciences, I recommend Tom Siegfried, The Bit and the Pendulum (Wiley, 2000), ISBN 0471321745 (hardback), 0471399744 (paper).
![]()
In this section, we do a bit of an aside. We consider a heat engine; all of our engines are examples of such a system.
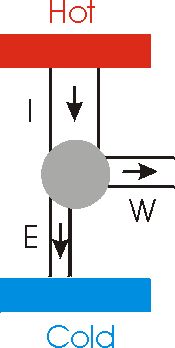 |
To the left we illustrate a generic heat engine. In common with all engines it takes input heat energy I from a hot area, produces some useful work W and deposits its exhaust E into a colder area Conservation of energy means I=W + E. |
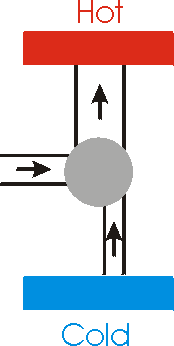 |
Now we illustrate a generalised refrigerator. It takes heat from the colder area plus some input energy and dumps the sum into the hotter area. |
|
Now we show on the right a heat engine that is 100% efficient: it takes all of its energy from the hot area and turns it into useful work. We take that work and use it to power a refrigerator. But if we consider the 100% efficient engine plus the refrigerator as a single system, the total effect is to take heat energy from the colder area and put it into the hotter area. This violates the Second Law of Thermodynamics. Thus, we conclude that a 100% efficient engine is impossible. |
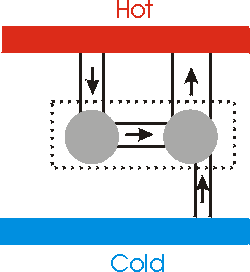 |
![]()
We often hear "experts" quacking about the energy crisis. A moment's consideration of the implications of E=m c 2 makes it clear that we have all the energy we can use.
The problem is one of entropy, not energy.
There is a device called a solarium: it is a large glass container in which is placed a mixture of soil, vegetation, snails, water, etc. You can take a solarium, seal it up, and put it in the sunlight; if it is properly devised it will basically live forever. However, if you take the solarium and put it in a dark closet very soon you will have a mush of foul-smelling high-entropy goo.
The key for the solarium is that when it is in the sunlight the system is unclosed; energy is flowing through the system. Put it in the closet, which closes the system, and the entropy gets it.
Similarly, for the Earth we got from a undifferentiated goo of chemicals to a highly ordered biomass of about a trillion kilograms. This transition from disorder to order does not violate the Second Law of Thermodynamics: the system's interaction with, particularly, the Sun means the system is not closed so the Second Law does not apply.
Now consider some common energy sources that we use or are trying to use: