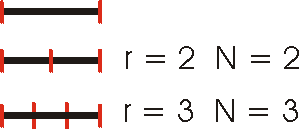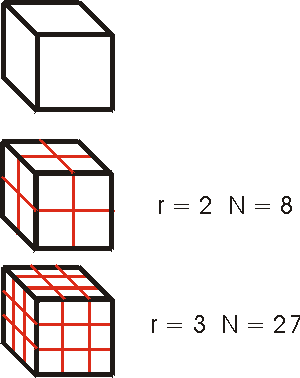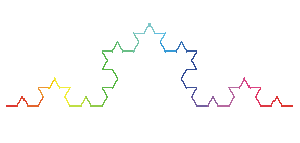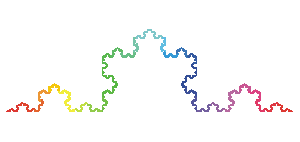Measuring Dimensions

The measurement of the dimensionality of an object rapidly gets fairly subtle. This is a brief and fairly simple introduction.

Hausdorff Method

Here we illustrate a method due to Hausdorff to measure the dimensionality of an object. We consider "normal" Euclidean objects: a line, a square, and a cube. For each we will reduce the scale of the object by a factor of r and add objects so that we fill the same space; we will end up with N objects.

Here is a one-dimensional line. First we reduce its size by a factor of two and fill the available space. We end up with two lines.

Next we reduce the size of the original line by a factor of three, and again fill the available space. We end up with three lines.

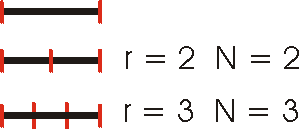 Dividing a line

Now we use a two-dimensional square.

 Dividing a sqaure

Finally, a three-dimensional cube.

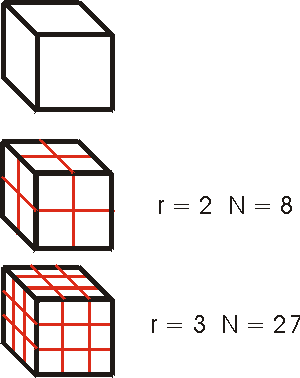 Dividing a cube

For each of these cases, note that N = r D, where D is the dimensionality of the object. This is the Hausdorff method for measuring dimensions.

The Koch Curve

We consider the "monster" Koch curve.

We begin with a line and replace it with four lines, each of which is one-third of the length of the original line

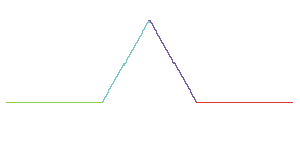 First iteration of Koch curve

Now we take each line segment from above and repeat the procedure.

 Second generation Koch curve

We repeat this procedure one more time.

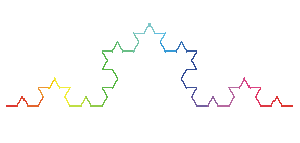 Third generation Koch curve

After 6 iterations, here is what we get.

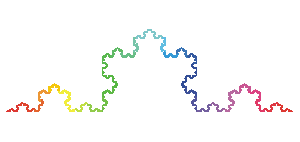 6 iterations Koch curve

The final result after an infinite number of iterations is the Koch curve. It can be shown that it will has an infinite length in a finite area. This property should remind you of, for example, the trajectory of the "Earth" in the three-body gravitational problem.

Let us try the Hausdorff method for the Koch curve. In the first first iteration, r = 3 and we end up with N = 4 line segments. The next iteration has r = 9 and N is 16. The next iteration has r = 27 and N = 64. For each iteration N = r D if the dimension D is the irrational number 1.26186.... So, the Koch curve has a non-integer dimension, and is a "fractal."

Coastlines of countries have been analyzed using this technique, and have similarly been found to be fractal.

Self-Similarity

One characteristic of the Koch curve we looked at above is that if we zoom in on the curve, at any magnification it looks exactly the same. This property of "self-similarity" is shared by all fractals. We discussed an example of the phenomenon when we were discussing the infinite levels of bifurcation the preceded the onset of chaos in the Logistic system. Leonardo da Vinci investigated this subject in the 16th century.

Trees, for example, exhibit some self-similarity. Here we draw a line, and then two shorter lines branching from its ends.

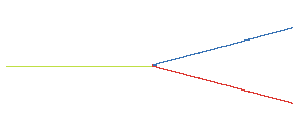 1st iteration of a tree

After the second iteration we get:

 2nd iteration of the tree

Here is the result after four iterations:

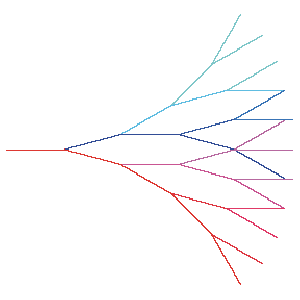 4th iteration of the tree

Finally, after six iterations:

 After 6 iterations

Although this tree also has fractional dimensionality, it turns out to be too complicated to determine by the Hausdorff method.

The text of this document is Copyright © David M. Harrison, 1998. This is version 1.3, date (m/d/y) 03/01/99. The Koch curve and tree graphics above were generated by Mathematica code written by Robert M. Dickau; his web site is accessible here.