Each part of a multipart question is of equal weight.
Show your work and reasoning; part marks will be given.
Useful information is given on the last two pages of this exam.
* Some of the following numerical constants may be useful:
| pi | p= 3.14159265358979323… | |
| speed of light | c = 299792458 m s-1 | |
| Planck's constant, reduced | h/2p = 6.58212x10-22 MeV s | |
| conversion constants | hc/2p = 197.327 MeV fm | (hc/2p)2 = .389379 GeV2 mb |
| conversion factors | 1 eV = 1.602177x10-19 J | 1 eV/c2 = 1.782662x10-36 kg |
| 1 barn = 10-24 cm2 | ||
| unified atomic mass unit | u = 931.494 MeV/c2 | |
| Avogadro's constant | NA = 6.022137x1023 mol-1 | |
| electron charge | e = 1.602x10-19 C | |
| electron magnetic moment | µe = 2.9665x10-7 eV-1 | |
| Boltzmann constant | k = 8.617x10-5 eV/Kelvin | |
| fine structure constant | a= 1/137.0360 | |
| strong coupling constant | aS(MZ)= 0.118±0.003 | |
| Cabibbo angle | sin qc @ Vus = 0.22 | |
| weak mixing angle | sin2qW= 0.2315 | |
| standard grav. accel., sea level | g = 9.8 m/s2 | |
| Hubble constant | H0=0.1 Gyr-1 | |
| neutral kaon mass difference | mKL- mKS = 3.510±0.018 meV | |
| Fermi weak coupling constant | GF = 1.166x10-5 GeV-2 | |
| Newton's (gravitational) constant | = 6.707x10-39 GeV-2 | |
| Z0 branching fractions | B.R.(Z0->e+e-)=3.21±0.07% | B.R.(Z0->hadrons) = 71±1% |
* Particle Properties *
| Boson | (GeV/c2) | Lepton | (MeV/c2) | Lifetime | (GeV/c2) | |||
| Hadron | Quark Content | Mass (MeV/c2) | I(JPC) |
| p0 | (u-d)/21/2 | 134.97 | 1(0-+) |
| p+, p- | u, d | 139.57 | 1(0-) |
| K+,K- | u, s | 493.65 | |
| K0, anti-K0 | d, s | 497.67 | |
| r+, r0, r- | u, (u-d)/21/2, d | 770 | 1(1--) |
| p | uud | 938.27 | |
| n | udd | 939.57 | |
| L | uds | 1115.6 | 0(1/2+) |
| S0 | uds | 1192.6 | 1(1/2+) |
| D-, D0, D+, D++ | ddd, udd, uud, uuu | 1232 | 3/2 (3/2+) |
| D0, anti-D0 | u, c | 1863 | 1/2 (0-) |
| D+,D- | d, c | 1869 | 1/2 (0-) |
| Lc | udc | 2285 | 0(1/2-) |
| B+,B- | u, b | 5279 | 1/2 (0-) |
| Lb | udb | 5640±50 | 0(1/2+) |
| Nuclei | Mass (in u) | Nuclei | Mass (in u) | Nuclei | Mass (in u) | ||
| H1 | 1.007825 | 2He3 | 3.01603 | 26Fe56 | 55.934939 | ||
| 1H2 | 2.0140 | 2He4 | 4.00260 | 82Pb208 | 207.976627 | ||
| 1H3 | 3.01605 | 6C12 | 12 |
Problem 1
(a) An electron accelerator is to be designed to study properties of linear dimensions of 1 fm. What kinetic energy is required?
(b) What is the magnetic moment of a hydrogen atom?
Problem 2
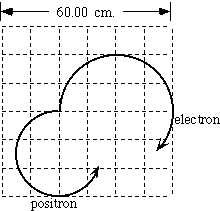
This is a sketch of a very rare two-body decay of a neutral particle.

The sketch has been reduced and a scale provided.The two particle
tracks shown lie in the plane of the paper; the initial angle
between the two tracks at the decay point is 90°. There is
a magnetic field of 3.33 Tesla (33,333 Gauss) perpendicular to
the page. What is the mass of the unknown particle? (You don't
need to calculate the uncertainty in the mass.)
Problem 3
Explain how Rutherford's alpha-gold scattering data showed that
the electric charge in atoms is not uniformly distributed over
the entire volume of the atom.
A isospin I=1 meson is observed to decay into 3 pions but not
into 2 pions. (a) Is the weak interaction responsible for
this decay? (b) What is the strangeness of the charged
meson?