Physics 357 : 1998 Lecture 22
The Strong Interaction
The simplest model for the strong interaction between hadrons (including nuclei) is that of
The forces between real billiard balls are contact forces between neutral atoms. These short range contact forces are due to the fact that neutral atoms are made from electromagnetically charged constituents. (Such forces - e.g. Van der Waals forces, atomic bonds - are general features of composite systems made charged constituents.)
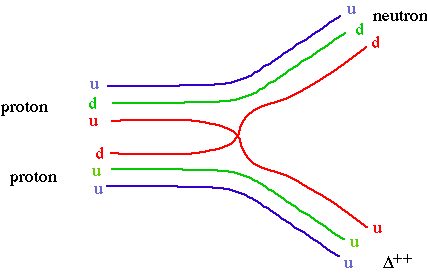
Since hadrons are made of constituent quarks, it is natural to expect that a short range force between hadrons can similarly viewed as due to

When such pairs of quarks are exchanged, the amplitudes are dominated by "poles" due the existence of quark-antiquark resonances, i.e. mesons. The lowest mass resonances dominate the exchanges, so low energy forces can be well described by
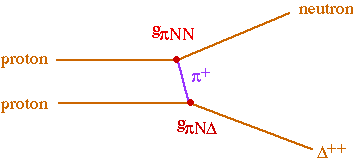
Yukawa predicted the existence of the pion based on the observed strong interaction isospin symmetry between protons and neutrons. (This symmetry is due to the fact that interchanging up and down quarks has only a very small effect on hadron properties.) In modern terms, we can describe pion exchange as an
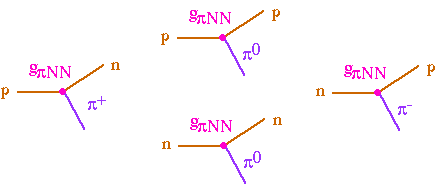
The philosophy behind the isospin theory
of the strong interaction was that isospin is a symmetry of the
strong interaction, so maybe isospin is
the charge of the strong interaction. This is a good effective
theory at low energies, but it breaks down at high energies because
neither nucleons or pions are point particles.
A more fundamental theory is
needed.
In the 1960's, colour was introduced to reconcile the quark model with fermi statistics. The basic problem was observed in the lowest lying baryon multiplets. The Pauli exclusion principle forbids identical fermions in the same quantum state, so how can the D++ (or D0 or W-) exist? The discovery of the Omega- confirmed the power of the quark model, so colour was introduced as a new quantum number associated with quarks. Colour makes it possible for the quark model to obey Fermi-Dirac statistics.
Colour was introduced to save the quark model, but it had the characteristics of an SU(3) gauge symmetry. (SU(3) is the group which corresponds to 3 by 3 unitary matrices.) Since colour is a quantum number associated with the quarks, and only quarks interact strongly, a local colour SU(3) gauge theory was (in hindsight) an obvious candidate for a fundamental theory of the strong interaction.
Almost all observed hadrons are consistent
with being either quark-antiquark mesons or 3 quark baryons.
Return to List of Lecture Notes