Physics 357 : 1998 Lecture 20
Charm Decays
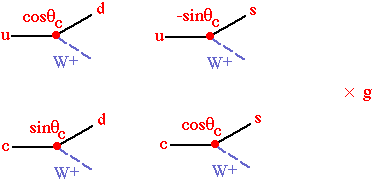
Charm does not exclusively decay into strange quarks, they also decay into down quarks about 5% of the time. If we only consider u, d, s, & c quarks, then the relative strength of the coupling amplitudes is parameterized by the Cabibbo angle, qc.

At this point we must define up, down, strange, and charm quarks:
These definitions are often referred to as the quark mass eigenstates. We are free to define either the "up" or "down" mass eigenstates as being weak eignestates. If we choose "up", then up and charm mass eigenstates are weak eigenstates, and then the down and strange weak eigenstates, d' & s', are defined to be the weak eigenstates coupling to u and c respectively:
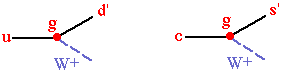
In terms of their mass eigenstates and the Cabibbo angle we have:

Measurements of the strength of nuclear beta decays relative to muon decays gives
measurements of the strength of strange particle decays give
and measurements of the strength of charm decays give
There are a total of 16 possible lowest order bare charm decays, and all decays involving quarks are subject to hadronic effects.
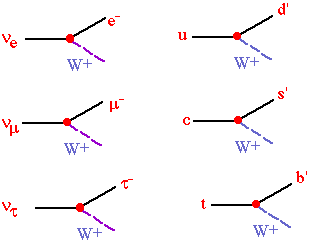
Weak couplings for 3 generations
The couplings of all known fundamental fermions:
where the Cabibbo-Kobayashi-Maskawa mixing matrix is
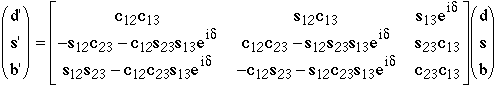
The notation for the CKM matrix varies. In this case, cij=cosqij, sij=sinqij, and there are 4 parameters: q12@ qc, q13, q23, and d. The additional quark mass eigenstates are:
The charged lepton mass eigenstates are:
Neutrino Oscillations
If neutrinos do not all have the same mass, then their mass and weak eigenstates may differ, and neutrino oscillations may occur. There is no conclusive evidence yet that the neutrinos do not all have zero (and hence equal) masses. There are, however, several experimental results which suggest such oscillations may occur. The best known and most solid evidence is from the Solar Neutrino Problem. The SNO experiment in Sudbury should be able to tell us whether solar neutrinos oscillate or just aren't there.
Return to List of Lecture Notes