Electromagnetism

• U(1) gauge interaction
• mediated by vector gauge boson (J^P=1^-)
  (corresponds to classical vector potential)
• coupling to electric charge with strength a=e²/4pe₀
• everything is conserved (e.g. E, p, j, Q, B, L, P, C, T, quark and lepton flavours except total isospin (since up and down quarks have different electric charges).

Perturbation Theory

If an interaction is weak (e.g. a << 1), then the rate for a given processs can be calculated perturbatively.

e.g. Total charged particle scattering rate =

Fermi's Golden Rules

Quantum mechanically, the lowest order rate can be calculated using Fermi's Golden Rules

Consider a system described by the time independent Schrödinger equation

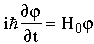
with stationary state eigen solutions

If there is a small interaction coupling different states, then H=H₀+H_int, and the lowest order transition rates can be calculated perturbatively

Direct transition from an initial state |aÒ to a final state |bÒ:

Fermi's Golden Rule No. 2

where

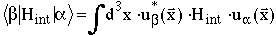
is the integral over space of the coupling of the space parts of the stationary states, and

is the density of states phase space

i.e. The transition rate is the square of the amplitude for interaction coupling the two states together times the phase space for the transition.

If there is no direct coupling between the initial and final states, the transition from an initial state a to a final state b via intermediate states n are given by:

Fermi's Golden Rule No. 1

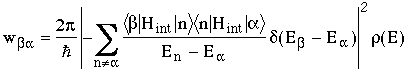
e⁺e^-->m⁺ m^-

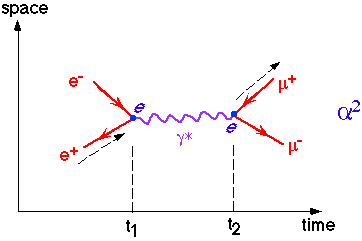
Consider the cross section for electron-positron annihilation into a muon pair via an intermediate virtual photon. There is no direct 4-fermion coupling between electrons and muons, i.e.

So the dominant mechanism is via a single intermediate virtual photon

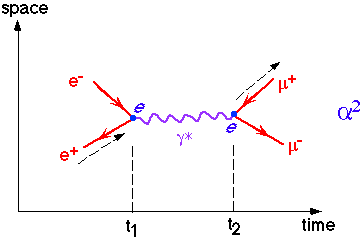
The total amplitude the sum of all possible time-ordered diagrams. In this case there is one additional possibility:

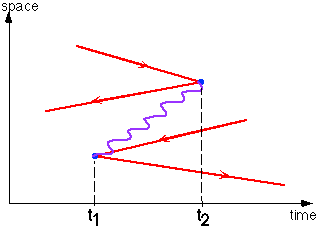
The total matrix element for e⁺e^-->m⁺ m^- is the sum of these two intermediate states, i.e.

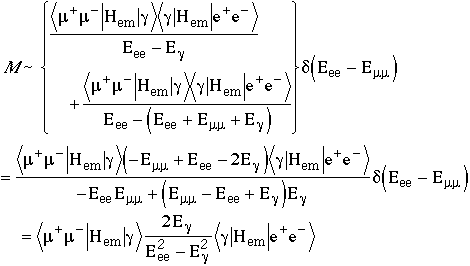
Where

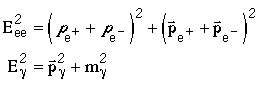
and

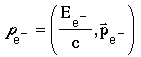
is the four-momentum of the electron, and similarly for the positron. Using 3-momentum conservation

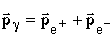
we then have that

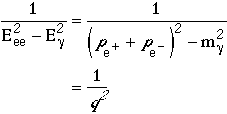
where q² is the 4-momentum-squared of the the virtual photon.

The gamma-fermion coupling terms are

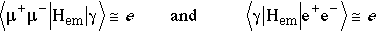
So we have that the matrix element is of the form

Feynman diagrams

In general, the exchange of a particle of mass m and 4-momentum p corresponds to a propagator term

in the matrix element

Relativistic quantum field theory is beyond the scope of this course, the amplitude of a process is calculated by drawing all the Feynman diagrams, writing down for each diagram the product of the vertex factors (couplings), the internal propagators due to exchanged particles, and factors corresponding to the polarization of the incoming and outgoing particles, and summing over all diagrams. The the total rate (e.g. cross section) is the square of the amplitude times the appropriate density of states factor and the cross section is of the form

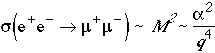
e⁺e^-->m⁺ m^- cross section

By counting the vertex and propagator factors, we see that the matrix element for electron-positron annihilation into muon pairs is of the form:

where q² is the four-momentum of the virtual photon.

The cross section is thus of the form

But this is dimensionally incorrect, so the phase space and other factors must have units of (energy)². In the high energy limit, where the masses of all the fermions can be neglected, the only relevant variable with units of energy is q². So the cross-section must be of order:

The correct total cross section for the annihilation of point electrons into point muon pairs via electromagnetic interactions is (in lowest order)

where s=q² is the square of the total c.m. energy of the electron-positron annihilation. In the c.m. frame, s=(2E_e²).

Muon size?

The size of the proton is measured by scattering electrons from proton targets. The size of the proton is parameterized by the form factor (See F&H equation 6.20):

Where a proton's or neutron's size is reasonably well parameterized (see F&H Fig. 6.15) by a "dipole" form factor (F&H equation 6.50)

corresponding to an exponential radial charge distribution (F&H Table 6.1) with mean radius R.

The size (or lack thereof) of muons could, in principle, be measured in the same way.

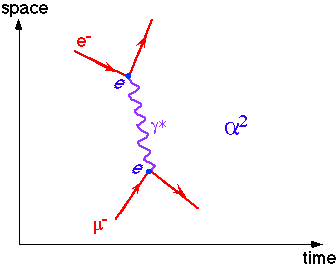
Scattering electrons from muons at high energy is not (yet) technically feasible, but the Feynman diagrams for scattering and annihilation are just the same diagram rotated 90°. This immediately tells us that in the high energy limit is

which is, of course, the expected and familiar result

Since the physics of annihilation is essentially the same as scattering, it is not surprising that we have the same sensitivity to form factors, i.e.

where, for example, a dipole form factor would be

Copyright 1998 David Bailey, University of Toronto