Antiparticles

Free particle wave equations are derived from kinematic laws using the quantum mechanical substitutions

For example

• non-relativistic Schrödinger equation

• relativistic Klein-Gordon equation

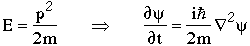
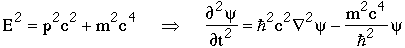
Any relativistic wave equation (e.g. Klein-Gordon or Dirac equations) has both positive and negative energy solutions

The negative energy solutions correspond to the motion of antiparticles; antiparticles must exist if quantum mechanics and special relativity are correct.

• Invariance under the combined CPT transformation requires that particles and their antiparticles must have equal masses and lifetimes.
• Particles and their antiparticles must have opposite "charges", i.e. electric charge, baryon number, lepton number, colour,….
• If a particle carries no charges, then it is its own antiparticle. e.g. g, p⁰, r⁰,…..
• C-invariance says that changing particles into antiparticles should not change the physics. If C invariance does not hold, then particles and their antiparticles do not have to interact the same way.

 Time Reversal (tÆ-t)

A wavefunction cannot be in an eigenstate of T, because T is an antiunitary operator which changes functions to their complex conjugate. e.g. if

then (using Tp =-p)

One can easily see that the eigenvalue equation

has no solutions, even for a complex eigenvalue l= re^iq.

This does not mean T may not be a symmetry of the Hamiltonian. It does mean that wavefunctions cannot be eigenstates of T.

Probabilities and expectation values are unchanged if T is a symmetry. e.g. For a free particle wave function

This may not be true for interactions if complex matrices are involved. T symmetry, as well as CP, is violated at the 0.2% level in neutral kaon decays.

Time reversal can be tested in several ways, for example, consider a two body reaction involving initial state spinless particles a & b, and final state spinless particles c & d:

Under time reversal we get

and applying parity we have

So PT symmetry would imply that the rate for the reaction a+b Þc+d should be the same as the rate for the reaction c+d Þa+b. This is the principal of detailed balance.

Symmetries and Conservation Laws

A system is said to have a symmetry if the laws of physics for that system are invariant under some transformation.

For example, if the laws of physics are independent of location in space, then if y(x) is a solution of the Schrödinger equation

then y (x+d) is also a solution, where d is a displacement in x. Consider an infinitesmal transformation, dÞ0. (This is quite general, since space translation is a continuous operation, so any arbitrary finite translation, D, can be made in infinitesmal steps.)

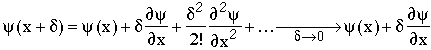
But remembering that the momentum operator is

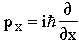
so

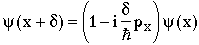
This must also be a solution of the Schrödinger equation

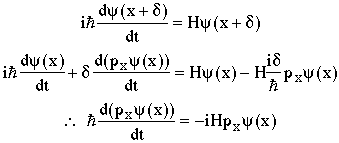
Something (e.g. F) is conserved if its expectation value is independent of time. Assume the operator F does not depend on t, then

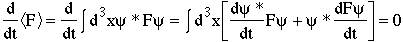
In this case, we have assumed space invariance and the momentum operator has appeared, so let's check

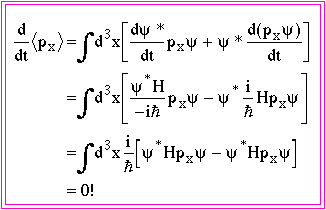
So the assumption that physics is invariant under space transformations requires that momentum be invariant!

In general such continuous symmetries give additive conservation laws.

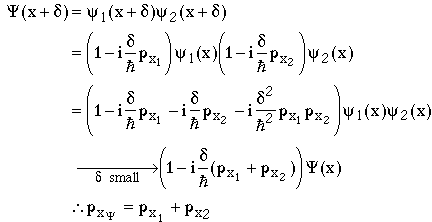
In general, if a operator commutes with the Hamiltonian, the corresponding observable is a conserved quantity.

e.g. Energy, momentum, and angular momentum conservation correspond to invariance under time and space translations, and space rotations.

Since these translations can be described by the Lorentz group, we can say that energy-momentum conservation are due to the Lorentz group symmetry of the universe.

Note, however, that we often write down Hamiltonians which do not conserve momentum or energy. e.g. When there is an external potential, or friction. In these cases momentum and energy may not be conserved, but this is because our wavefunction does not include the whole system.

"Charge" Conservation

Conservation of "charges" such as electric charge, baryon number, lepton number, strangeness, … correspond to invariance under various continuous symmetry transformations.

(Note: A continuous symmetry may correspond to a charge which happens to be discretely quantized. Such quantization is due to the charges of the fundamental particles; it is not an intrinsic consequence of charge conservation or the corresponding symmetry.)

For example, consider electric charge conservation. Let Q be the electric charge operator with eigenvalues q, i.e.

Electric charge conservation is equivalent to saying that there is a symmetry under continuous transformations of the form

where e is an arbitrary parameter. This is known as a U(1) gauge transformation, where U(1) is the name of the mathematical group describing the characteristics of the transformation.

This transformation is just the finite version of an infinitesimal transformation:

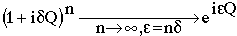
Transforming our normal free particle Hamiltonian we have

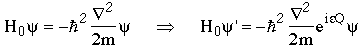
This is known as a global U(1) gauge transformation if e is the same at all points in space & time.

We can easily see that the free particle Schrödinger equation is invariant under the U(1) gauge transformation

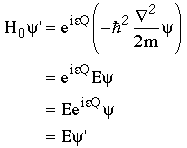
so electric charge is a conserved quantity in exact analogy with our previous discussion of momentum.

Saying that there is a global symmetry is equivalent saying there is a conserved quantity. Things become more interesting if we ask if there is invariance under local U(1) gauge transformations, where we allow e to vary locally in space and time, i.e. e= e(x,t) is an arbitrary function. Then we have

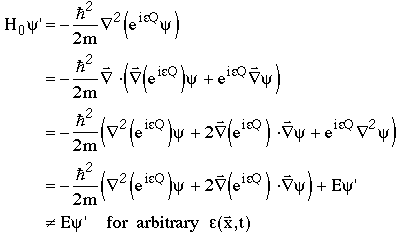
So local U(1) gauge invariance does not hold for our free particle wave equation.

But what if we insist?

The only way to make U(1) gauge invariance true is to change the Hamiltonian. In fact, we must add vector and scalar fields to the Hamiltonian so that the new Hamiltonian is

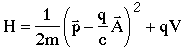
where A(x,t) and V(x,t) transform under U(1) gauge transformations such that

So

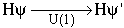
where

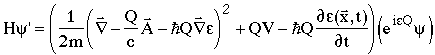
so

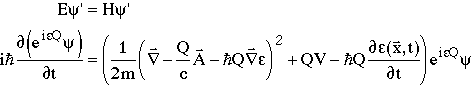
This Hamiltonian has exactly the form of the Hamiltonian of an electrically charged particle in a vector and scalar electromagnetic potential.

i.e. Requiring local U(1) gauge invariance requires that the particle interact with a field. In this case all of electromagnetism can be summed up by saying there is a local U(1) gauge invariance of the universe.