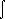Quantum Scattering

Born approximation: incident particle is a plane wave and scattered amplitude is a spherical wave.

In general, the differential cross-section can be written as

where f(q) is essentially the Fourier transform of the scattering potential

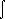f(q) = -(m/2p) V(r) e^iq·r d³r

If the scattering is spherically symmetric

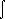f(q²) = -(m/2p) V(r) r sin(qr) dr

If V(r)~1/r, then simple dimensional counting requires f(q²)~1/q².

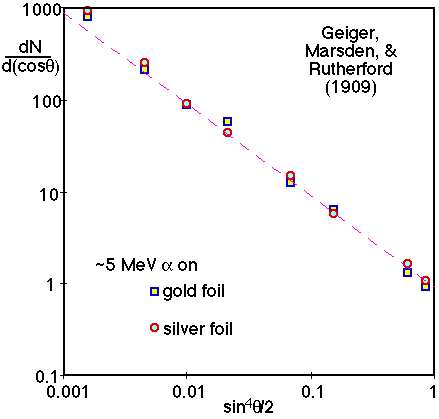
Rutherford scattering can be analysed either classically or quantum mechanically.

In general, if there is no range or size scale in a scattering problem, then dimensional analysis requires

Which is very different from the the differential cross section expected from billiard ball scattering (ds/dW µ constant).

For electromagnetic scattering of incident point particles, we can consider scattering from an extended target as point-point scattering integrated over the charge distribution of the target:

The Form Factor is the Fourier transform of the target's charge distribution:

F(q²) = r(r) e^iq·r d³r

and (ds/dW)_R is the reference cross section for poin-point scattering (e.g. For electron scattering this is usually Mott scattering, but Rutherford scattering can be used in the low energy limit.)

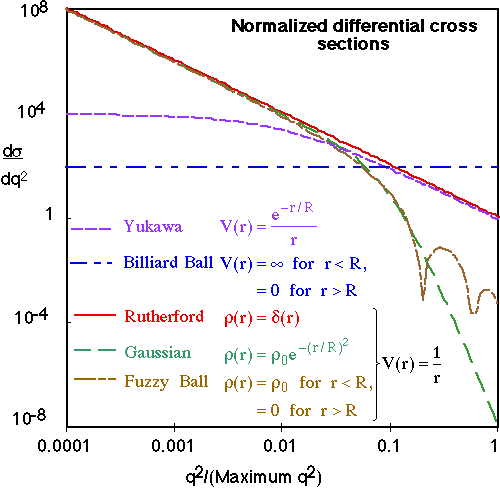
Comparison of differential cross sections for scattering a spinless point particle from either a Rutherford point particle or particles with a size R=10/q_max.

Electron-proton scattering

F&H Figure 6.13: the proton is not a point electric charge, but has a size ~1fm.

F&H Figure 6.5: atomic nuclei have a size and a reasonable well defined edge.

F&H Figure 6.19: protons do not have a well defined edge, but inside the proton there seem to be point charge constituents.