Magnetic moments and Structure

Electromagnetic dipole moments are typically

For point particles, the intrinsic length is the Compton wavelength (i.e. 1/m)

Classically, the magnetic moment of a particle in a circular orbit with angular momentum L is

Subatomic particle magnetic moments are usually written

• For a classical point particle: g = 1
• For structureless spin-1/2 point fermions: g = 2
• For structureless neutral particle: m = 0

	Particle	gmeasured	gpoint(QED theory)
	electron	2.002319304377(4)	2.002319304402(54)
	muon	2.0023318480(170)	2.0023318412(40)
	proton	5.58569478(12)	2.002
	neutron	m = 3.8260856(10) mN	0

Deviations from g=2 indicate that the fermion has structure. Even point fermions have a some structure due to the constant radiation and absorption of photons.

Protons and neutron do not have point particle dipole moments because they are not point particles. The magnetic moments of particles made from bound consituents are typically:

where the sum is over all the constuents. The effective mass of a constituent, m_i(eff), depends on the intrinsic mass, m_i, and on the binding forces on the constituents, i.e.

In an atom, the magnetic moments of paired (spin up - spin down) electrons cancel out, and the binding energy of any unpaired electron is typical 10 eV. In a nucleon, the the binding forces contribute several hundred MeV to the effective masses of the constituent quarks. If the constituents are not in an S-wave state, one would also expect contributions to the magnetic moment of order Q_i·R, where R is the size of the particle.

Magnetic moments provide indirect but very powerful information about particle structure. Even in the undergraduate lab, measurements of Electron spin resonance and Nuclear magnetic resonance indicate that electrons are point particles and protons are not.

Scattering experiments are used to directly measure the size and substructure of particles.

Rutherford's Experiment

Consider a light charged particle approaching a infinitely massive (i.e. fixed) charged particle.

The energy, U, needed for particle m to approach within a distance r of the target particle M is

If the target particle is a uniform charged sphere of radius R

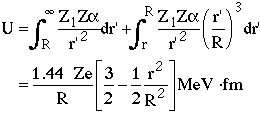
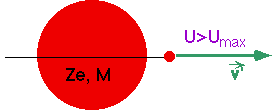
Rutherford thought: R~1Å (atom size), Z₁=2 alpha particles, Z=79 gold foil.

but the alphas had kinetic energies ~5.5 MeV, so Rutherford observed backscattering

(Billiard balls, or any hard interaction, can scatter up to the kinematically allowed maximum).

In order to resolve this issue more data and more detailed analysis are necessary.

Classical Billiard Ball Scattering

An example of scattering via a strong, short range (contact) force (cf. Rutherford scattering).

Non-relativistic elastic scattering of a billiard ball (mass m, radius R) from a fixed (infinitely massive) billiard ball (radius R also).

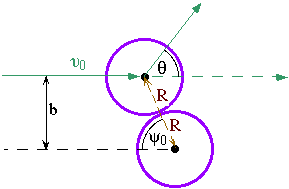
By geometry, the angle y₀ at the point of closest approach (i.e. the point of contact) is given by

and the scattering angle is

Consider a parallel beam of billiard balls with velocity v₀ incident on a thin target which contains n target balls per unit volume and has a thickness L. Let N₀ be the number of balls incident per unit area of the target. For a thin target, the number of particles incident with impact parameters between b & (b+|db|) will be dN= N₀(2pb |db|)(nL); this is also the number of particles per unit area into an angular cone between q & (q +d q), so using

we get

The scattering is independent of j, so it is uniform over j=0 to 2p, and so the number of particles scattered into a solid angle dW=dj sinq dq is

The flux of balls per unit time through unit area normal to the beam is

where n_ball is thedensity of balls in the beam. (N₀=F dt, where dt is a time interval). The rate of scattering per unit target ball per unit time is thus

The scattering rate per unit target ball is

where

is known as the differential cross section. In general, the scattering or interaction rate for any process per target particle is

i.e. s parameterizes the scattering probability and is known as the cross section. The total cross section is

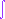s = (ds/dW) dW = 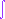R²dj sinq dq = 4pR²

as expected

The differential cross section can be also written in terms of the momentum transfer in the collison, q, i.e.

For elastic scattering (p_f=p₀)

Since the cross section is independent of j, we can it integrate out (j=0 to 2p)

In this case the differential cross section is constant

up to the maximum momentum transfer when a ball scatters straight back, i.e. p_f = -p₀ and q²_max = 4p₀²

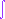s_tot = pR²/p₀² dq² = 4pR²

once again as expected