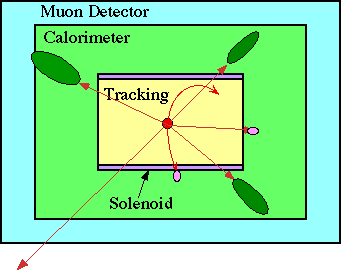
Subatomic Physics Detectors

Measure for every particle produced in an interaction.

position	(x, y, z)
momentum or energy/angle	P or (E,q,f)

mass	m
electric charge	Q

Tracking detectors measure the positions of charged particles.

A solenoid provides a magentic field so the momentum of charged particles can be determined from their radius of curvature.

Calorimeters measure the energy of hadrons, photons, and electrons.

Muon detectors identify muons because muons and neutrinos are the only particles which can pass through the the calorimeters, but muons ionize and neutrinos don't.

Measuring energy

Calorimeters measure energy by absorbing particles. Most calorimeters measure the ionization energy deposited by all the charged particles in the "showers" produced as the particle is absorbed. The scale length of electromagnetic showers is the radiation length, X₀ (~2cm in Fe), relevant for both bremstrahlung pair production; the scale length for hadronic showers is the mean hadronic interaction length, l_I (0.2m in Fe).

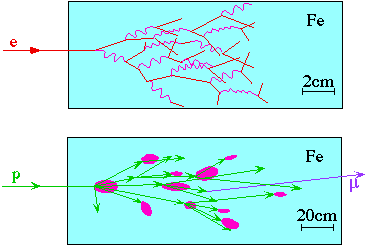
Ionization observed is proportional to energy lost

This is statistical process

The resolution degrades rapidly if all the particles are not absorbed. i.e. The fluctuations in how much energy leaks out can be much bigger than the statistical uncertainty on measuring the energy that does not leak out.

 Photons from Natural Radioactivity observed with a Germanium semiconductor detector

The common natural radioactive isotopes are Potassium-40, Uranium-235, Uranium-238, and Thorium-232.

Natural potassium (Z=19 protons) has 3 isotopes (N=20, 21, or 22 neutrons):

ZKA=N+Z	Natural Abundance	Half-life
19K39	93.3%	stable
19K40	0.012%	1.25x109y
19K41	6.7%	stable

Potassium-40 decays (from National Nuclear Data Center and Table of Nucleides):

Decay		%	DE (MeV)
b-	19K40 Þ 20Ca40+e-+e	89.3	1312
b+	19K40 Þ 18Ar40+ e++ne	0.001	1505
electron capture	19K40 + e-atomic Þ 18Ar40*+ne      (18Ar40*Þ 18Ar40+g)	10.7	1505 (1461)

Beta decay

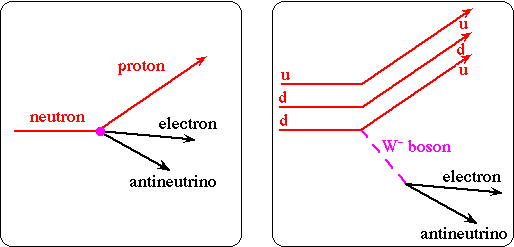
If particles can decay to a lower energy state, they will. Looking at some mass 40 isobars we can predict which isotopes will undergo beta decays:

	Isotope	Mass Excess = (M-A·u)
	17Cl40	-27.558 MeV
	18Ar40	-35.040 MeV
	19K40	-33.535 MeV
	20Ca40	-34.846 MeV
	20Sc40	-20.526 MeV

atomic mass unit (u) = (mass ¹²C atom)/12 = 931.49432(28)MeV

A typical 70kg human body has 140g of potassium, and 17mg of K⁴⁰, corresponding to a decay rate of 4.4kBq, and an annual dose of about 0.2mSv (out of a typical total of about 3.6mSv).

	SI Unit	Old Units
Activity:	Bequerel (Bq) = 1 decay/s	Curie (Ci)=     3.7x1010 Bq
Absorbed Dose	Gray (Gy) = 1 Joule/Kg	Rad = 0.01 Gy
Equivalent Dose	Sievert (Sv) = Gray x Q    (Q = radiation       weighting factor)	Rem = 0.01 Sv

Photon Interactions

Photon total cross sections in Carbon (Z=6) and Lead (Z=82), showing the dominant contributions for carbon.

• s_p.e - photoelectric effect
• s_compton - Compton Scattering
• s_pair - pair production

Pair production

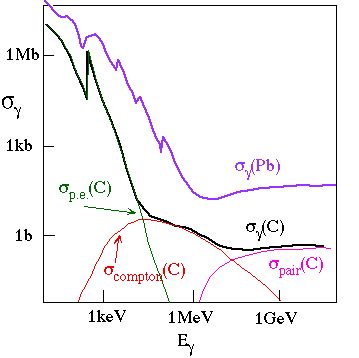
Real photons spend part of their time (about a) as a virtual electron-positron pair. These virtual e⁺e^- pairs can scatter from the virtual photons in the electromagnetic field of a charged particle, e.g. an atomic nucleus or electron, and become a real e⁺e^- pair.

In the high energy limit (E_g>>2m_e), the mean distance a photon will travel before pair producing is

(Note: The reason the radiation length and the pair production length are almost the same is because bremsstrahlung and pair production are simply time and space rearrangements of the same process: a real photon coupling to an electron which is coupled via a virtual photon to a nucleus.)