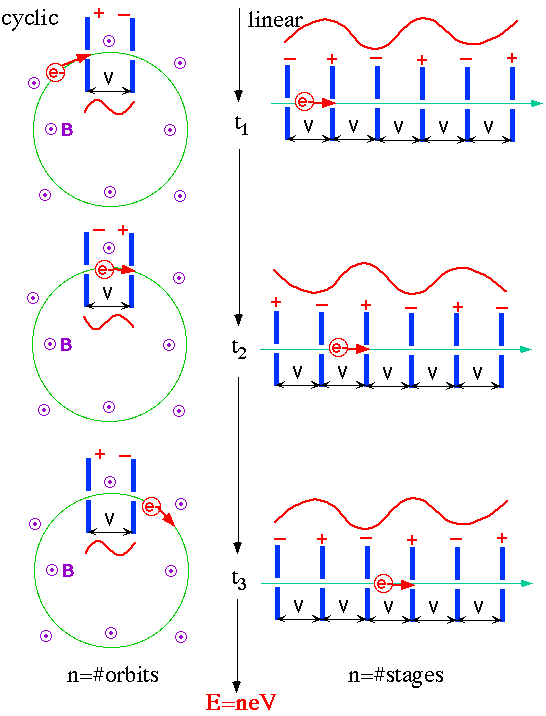
Repetitive Acceleration: Cyclic or Linear

In general, static magnetic fields are much stronger than static electric fields. The Lorentz electromagnetic force law

tells us that a 1 Tesla magnetic field exerts the same force on a relativistic particle (v@c) as a 3x10⁸ Volt/metre electric field. This can also be seen by looking that the units, i.e.

Using the conversion constant c = 3x10⁸ m/s, we have 1m/s = 1/(3x10⁸), so

It is easy to generate a 10T (= 3x10³ MV/m) static magnetic fields, but static electric fields above about 3 MV/m are almost impossible. This is because our world is made from particles with electric charge but no magnetic charge, so high electric fields are shorted out by sparks consisting of electrically charged particles. There is no known reason why magnetic charges ("magnetic monopoles") should not exist, and they probably do but very rarely and with masses of the order of 10¹⁵ GeV/c².

Sychrotrons

• ring of magnets
• small amount of radiofrequency (r.f.) acceleration
• magnetic field increases synchronously with beam momentum,

      B = p/(|q|r)

Example: Fermilab Tevatron

• r = 1 km
• B = 0 - 5 Tesla
• DE/orbit ~ 3 MeV    (10m @ 1/3 MV/m)

Effective Accelerating Gradient

G

=

final particle energy length of accelerator

for a synchrotron

		G	=	Emax/2pr
			@	pmaxc/2pr   (E>>m)
	\	G (J/m)	=	|q|rBmaxc/2pr   (SI)
			=	|q|cBmax/2p
	\	G (eV/m)	=	|q/e|cBmax/2p   (1.6x10-19 = C/e = J/eV)
		G	=	(48 MeV/Tesla)·Bmax

e.g.

   Tevatron:  G ~ 150 MeV/m,

   LHC:     G ~ 250 MeV/m

Limits to circular accelerators

  protons
     - size ($$)
     - B (H_c, stress µ B²)
     - S/N (s_new ~ 4p/E², s_stotal ~ 10² mb)

  electrons
     - synchrotron radiation

        energy loss / orbit
            = (4p/3) e² b² g⁴/r
            = 88.5x10^-6 [E(GeV)]⁴/r(m)

          e.g. 88.5 TeV/orbit if E=1TeV and r=1km

Acceleration by Electromagnetic Waves

Power per unit area of an electromagnetic wave (Poynting Vector)

In vacuum: E_max=cB_max, but E & B are 90° out of phase, so

So the maximum electric field is

e.g. 10²⁰ W/m² Þ E_max= 275 GV/m

But in free space E is transverse to the direction of propagation of the wave, so there can be no continuous acceleration, just oscillation.

Linear Acceleration

e.g. SLAC (e^± linac)

    Fermilab proton linac injector

Typical limits on accelerating gradients for copper structures (e.g. SLAC disk-loaded waveguide).

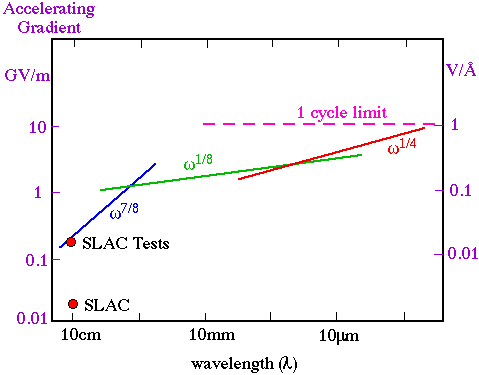
c.f. static breakdown voltage of dry air = 3 MV/m