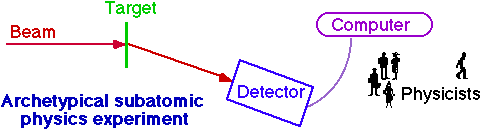
Experimental Subatomic Physics
* Some subatomic physics experiments look in nature to study naturally occurring subatomic processes
* but most experiments usually bang things together to see:
* In order to extract this information from experiments,
* After analysis, the results are expressed as

| Rutherford | CDF | |
| team | Geiger(RA), Marsden(UG) | cast of thousands |
| beam | a particles
(Rd, ~5 MeV) | antiprotons/protons (Tevatron, 900 GeV) |
| target | foil (Au,Ag) | proton/antiproton beam |
| detector | ZnS screen + eyeball | 10000 ton hermetic detector |
| data acquisition | pencil | networks, workstations, disks, tapes, .... |
| analysis | student+pencil | ~102 students + computers |
Starting with ordinary matter (electrons, nucleons, photons), we want to probe smaller and smaller distance scales and produce new states of matter.
We use accelerators to produce our high energy probes, and detectors to observe what happens.
Accelerators
electromagnetic energy (electromagnetic fields, waves)
Þ energetic (charged) particles
Detectors
energetic (charged) particles
Þ electromagnetic energy (light, charge)
In order to do physics, an accelerator must provide us with:
(1) energy
l=hc/E , E>2m
(2) luminosity
Rate (s-1) = s (cm-2) L (cm-2 s-1)
The cross-section (s) parameterizes the probability of an interaction. e.g. billiard balls
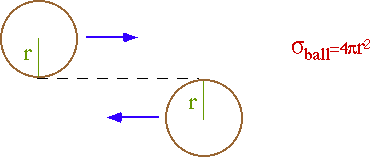
For point particles (r ~ l) interacting by a point interaction (range ~ l):
Unitarity Limit
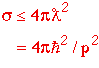
So if we want to see the same number of interactions as we increase the energy, we must have
e.g. Consider two bunches of particles colliding head on. If the particles in each bunch are uniformly distributed over an cross sectional area A, the probability of any two particles travelling in opposite directions interacting is just s/A. The total number of collisions between particles in the two bunches is then (s/A)N1N2, where N1 and N2 are the number of particles in each bunch. If bunches of particles are colliding with a frequency, f, then the total collision rate is R = (s/A)N1N2f, so the luminosity is
Simplest Accelerator
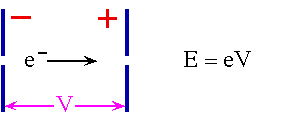
but
